Выполнение предпосылки МНК о гомоскедостичности остатков. Тест Голдфилда-Кванта.(с50-53)
Условие независимости факторов м/у собой.
Нарушение данного условия, когда факторы зависят друг от друга, называется мультиколлинеарностью. Нарушение условия 4 является нарушением одного из требований классической регрессии. Мультиколлинеарность проверяется на основе коэффициента корреляции Для того чтобы мультиколлинеарности не было д.б. Мультиколлениарность возникает из-за неисправного выбора списка объясняющих переменных или из за эконом.природы выбранных переменных. Внешние признаками мультиколлениарности явл.следующие признаки: 1) наличие значений коэффициентов парной корреляции м/у объясняющими переменными, превышающих по модулю 0,75. 2) Наличие оценок коэффициентов регрессии, имеющих непрерывные знаки. 3) Существенные изменения значений коэффициентов регрессии при небольшом изменении исходных данных. 4) Наличие больших стандартных ошибок и малой статической значимости коэффициентов регрессии при общей значимости модели. Для устранения мультиколлениарности существует несколько способов: 1. исключение из модели связанных м/у собой независимых переменных путем отбора наиболее существенных объясняющих переменных. использование методов оценки коэффициентов, учитывающих мультиколлениарность Явление гетероскедастичности возникает, как правило, при анализе неоднородных объектов. Например, при построении зависимости прибыли фирмы от размера основного фонда (или каких-либо других факторов) гетероскедастичность вызвана тем, что у больших фирм колебания прибыли будут выше, чем у малых. МНК при наличии гетероскедастичности позволяет получить несмещенные оценки параметров модели, но оценка дисперсии ошибки, и, следовательно, границы доверительных интервалов оценок параметров модели и прогноза зависимой переменной будут неверными, т.к. они вычисляются на основании предположения гомоскедастичности ошибок. Для проверки на гетероскедастичность существует большое число тестов. Мы остановимся на тесте Голдфельда-Квандта. Тест Голдфелъда-Квандта применяется в том случае, когда имеются предположения: 1. о прямой зависимости дисперсии σt, ошибки регрессии εt от величины некоторой независимой переменной X в наблюдении t; 2. случайный член εt, распределен нормально и не подвержен автокорреляции. Алгоритм теста: 1. Упорядочивание n данных в выборке по величине независимой переменной, относительно которой есть подозрение на гетероскедастичность. 2. Исключение с средних наблюдений в этом упорядочении в целях построения двух независимых "частных" регрессий по данным n' = (n-с)/2 в начале выборки и по данным n' = (n - с)/2 в конце выборки 3. Проведение двух независимых "частных" регрессий - первых n' и последних n' наблюдений и построение соответствующих остатков е1 и е2; 4. Вычисление сумм квадратов остатков "частных" регрессий: е1'е1, е2'е2. Если предположение относительно природы гегероскедастичности верно, то дисперсии ошибок регрессии в последних n' наблюдениях будут больше (меньше), чем в первых n' наблюдениях при прямой (обратной) пропорциональной зависимости между σt и Xt и это скажется на сумме квадратов остатков в рассматриваемых частных регрессиях. Поэтому в качестве теста на выявление гетероскедастичности остатков регрессии предлагается использовать статистику F, вид которой определяется предположением зависимости между дисперсией ошибок регрессии σt и регрессором Xt: F = е1'е1 / е2'е2- в случае обратной пропорциональности F = е2'е2 / е1'е1- в случае прямой пропорциональности. Статистика F имеет распределение Фишера с (n'- k- 1) степенями свободы, где k- число объясняющих переменных в регрессионном уравнении. Если значение статистики превышает критически значение при определенном уровне значимости, то нулевая гипотеза Н0 об отсутствии гетероскедастичности отвергается. Тест ранговой корреляции Голдфелда-Квандта позволяют обнаружить лишь само наличие гетероскедастичности, но они не дают возможности проследить количественный характер зависимости дисперсий ошибок регрессии от значений регрессоров и, следовательно, не представляют каких-либо способов устранения гетероскедастичности. При использовании этого теста предполагается, что дисперсии ошибок регрессии представляют собой одну и ту же функцию от наблюдаемых значений регрессоров, т.е. s2 = fi (xi), Чаще всего функция f выбирается квадратичной, что соответствует тому, что средняя квадратичная ошибка регрессии зависит от наблюдаемых значений регрессоров приближенно линейно. Гомоскедастичной выборке соответствует случай f = const.
|


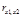

 (1)
(1)


