Показатели качества подгонки для многофакторной линейной регрессии. Частные коэффициенты эластичности.
Среди нелинейных функций, которые могут быть приведены к линейному виду, в эконометрических исследованиях очень широко используется степенная функция:
Связано это с тем, что параметр bв ней имеет четкое экономическое истолкование, т. е. он является коэффициентом эластичности. Это значит, что величина коэффициента bпоказывает, на сколько процентов изменится в среднем результат, если фактор изменится на 1 %. Например, если зависимость спроса от цен характеризуется уравнением вида В силу того, что коэффициент эластичности для нелинейной функции не является величиной постоянной, а зависит от соответствующего значения х, то обычно рассчитывается средний показатель эластичности по формуле:
Поскольку коэффициенты эластичности представляют экономический интерес, а виды моделей не ограничиваются только степенной функцией, приведем формулы расчета коэффициентов эластичности для наиболее распространенных типов уравнений регрессии. КОЭФФИЦИЕНТЫ ЭЛАСТИЧНОСТИ ПО РАЗНЫМ ВИДАМ РЕГРЕССИОННЫХ МОДЕЛЕЙ. 1. Линейная 2. Парабола 2 порядка 3. Гипербола 4. Показательная 5. Степенная 6. Полулогарифмическая 7. Логистическая 8. Обратная Несмотря на широкое использование в эконометрике коэффициентов эластичности, возможны случаи, когда их расчет экономического смысла не имеет. Это происходит тогда, когда для рассматриваемых признаков бессмысленно определение изменения значений в процентах. Например, вряд ли кто будет определять, на сколько процентов может измениться заработная плата с ростом стажа работы на 1 %. Или, например, на сколько процентов изменится урожайность пшеницы, если качество почвы, измеряемое в баллах, изменится на 1 %. Уравнение нелинейной регрессии, так же как и в линейной зависимости, дополняется показателем корреляции, а именно индексом корреляции (R):
Величина данного показателя находится в границах: 0 ≤ R ≤ 1, чем ближе к единице, тем теснее связь рассматриваемых признаков, тем более надежно найденное уравнение регрессии. Поскольку в расчете индекса корреляции используется соотношение факторной и общей суммы квадратов отклонений, то R2 имеет тот же смысл, что и коэффициент детерминации. В специальных исследованиях величину R2 для нелинейных связей называют индексом детерминации. Оценка существенности индекса корреляции проводится, так же как и оценка надежности коэффициента корреляции.
|


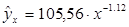 , то с увеличением цен на 1 % спрос снижается в среднем на 1,12 %.
, то с увеличением цен на 1 % спрос снижается в среднем на 1,12 %.
 .
. .
. .
. .
. .
. .
. .
. .
. или
или 



