Нелинейная регрессия. Виды нелинейных зависимостей. Линеаризуемые и нелинеаризуемые функции.
Если между экономическими явлениями существуют нелинейные соотношения, то они выражаются с помощью соответствующих нелинейных функций: например, равносторонней гиперболы, параболы второй степени и др. Различают два класса нелинейных регрессий: § регрессии, нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам; § регрессии, нелинейные по оцениваемым параметрам. Примером нелинейной регрессии по включаемым в нее объясняющим переменным могут служить следующие функции: · полиномы разных степеней – у = а + bх + с2 + ε, у = а + bх + сх + dx3 + ε,
§ равносторонняя гипербола К нелинейным регрессиям по оцениваемым параметрам относятся функции: § степенная — y = axb ε
§ показательная – у = аbх ε § экспоненциальная – y = ea+bx ε Приведение к линейному виду регрессий, нелинейных по объясняющим переменным Нелинейная регрессия по включенным переменным не таит каких-либо сложностей в оценке ее параметров. Она определяется, как и в линейной регрессии, методом наименьших квадратов (МНК), ибо эти функции линейны по параметрам. Так, в параболе второй степени у = а0 + а1 х + а2 х2 + ε заменяя переменные х1 = х, х2 = х2, получим двухфакторное уравнение линейной регрессии: у = а0 + а1 х1 + а2 х2 + ε для оценки параметров которого, как будет показано далее, используется МНК. Следовательно, полином любого порядка сводится к линейной регрессии с ее методами оценивания параметров и проверки гипотез. Среди класса нелинейных функций, параметры которых без особых затруднений оцениваются МНК, следует назвать хорошо известную в эконометрике равностороннюю гиперболу
Для равносторонней гиперболы такого вида, заменив Она может быть использована не только для характеристики связи удельных расходов сырья,материалов,топлива с объемом выпускаемой продукции, времени обращения товаров от величины товарооборота, т.е. на микроуровне, но и на макроуровне. Классическим ее примером является кривая Филлипса, характеризующая нелинейное соотношение между нормой безработицы х и процентом прироста заработной платы у. В отдельных случаях может использоваться и нелинейная модель вида
так называемая обратная модель, являющаяся разновидностью гиперболы Но, если в равносторонней гиперболе преобразованию подвергается объясняющая переменная z = 1 /x и y = а + bz + ε, то для получения линейной формы зависимости в обратной модели преобразовывается у, а именно: z =1 /y и z = a + bx +ε. В результате обратная модель оказывается внутренне нелинейной и требование МНК выполняется не для фактических значений признака у, а для их обратных величин 1 /у, а именно
следовательно полученная методом наименьших квадратов оценка уже не будет эффективной. Приведение к линейному виду регрессий, нелинейных по параметрам Данный класс нелинейных моделей подразделяется на два типа: нелинейные модели внутренне линейные и нелинейные модели внутренне нелинейные. Если нелинейная модель внутренне линейна, то она с помощью соответствующих преобразований может быть приведена к линейному виду. Если нелинейная модель внутренне нелинейна, то она не может быть сведена к линейной функции. Например, в эконометрических исследованиях при изучении эластичности спроса от цен широко используется степенная функция: y = axb ε где у – спрашиваемое количество; х – цена; ε – случайная ошибка. Данная модель нелинейна относительно оцениваемых пaраметров, ибо включает параметры а и b неаддитивно. Однако ее можно считать внутренне линейной, ибо логарифмирование данного уравнения по основанию е приводит его к линейному виду: lп у = lп а + b ln x + ln ε. Соответственно оценки параметров а и b могут быть найдены МНК. Если же модель представить в виде y = axb ε, то она становится внутренне нелинейной, ибо ее невозможно превратить в линейный вид. Внутренне нелинейной будет и модель вида — у = а + bхc + ε, ибо это уравнение не может быть преобразовано в уравнение, линейное по коэффициентам. В специальных исследованиях по регрессионному анализу часто к нелинейным относят модели, только внутренне нелинейные по оцениваемым параметрам, а все другие модели, которые внешне нелинейны, но путем преобразований параметров могут быть приведены к линейному виду, относятся к классу линейных моделей. В этом плане к линейным относят, например, экспоненциальную модель y = еa+bх ε, ибо логарифмируя ее по натуральному основанию, получим линейную форму модели ln у = а + b х +lnε. Среди нелинейных функций, которые могут быть приведены к линейному виду, в эконометрических исследованиях очень широко используется степенная функция y = axb ε. Связано это с тем, что параметр b в ней имеет четкое экономическое истолкование, т. е. он является коэффициентом эластичности. Это значит, что величина коэффициента b показывает, на сколько процентов изменится в среднем результат, если фактор изменится на 1%. В моделях, нелинейных по оцениваемым параметрам, но приводимых к линейному виду, МНК применяется к преобразованным уравнениям. Если в линейной модели и моделях, нелинейных по переменным, при оценке параметров исходят из критерия
то в моделях, нелинейных по оцениваемым параметрам, требование МНК применяется не к исходным данным результативного признака, а к их преобразованным величинам, т. е. lп у, 1 /у. Так, в степенной функции y = axb ε МНК применяется к преобразованному уравнению lп у = lnа + x ln b. Это значит, что оценка параметров основывается на минимизации суммы квадратов отклонений в логарифмах:
Вследствие этого оценки параметров для линеаризуемых функций МНК оказываются несколько смещенными. При исследовании взаимосвязей среди функций, использующих ln у, в эконометрике преобладают степенные зависимости – это и кривые спроса и предложения, и кривые Энгеля, и производственные функции, и кривые освоения для характеристики связи между трудоемкостью продукции и масштабами производства в период освоения выпуска нового вида изделий, и зависимость валового национального дохода от уровня занятости. 36.Нелинейные методы оценивания регрессии.Итерационные процедуры: Квази-Ньютоновский, симплексный и Розенброка методы. Функцией потерь или ошибок называется функционал вида
Также в качестве функции потерь может быть использована сумма модулей отклонений наблюдаемых значений результативного признака у от теоретических значений?:
Функция потерь характеризует потери в точности аппроксимации исходных данных построенной моделью регрессии. В интересах исследователя минимизировать функцию ошибок. Для этого используются различные методы, однако, их общий недостаток заключается в наличии локальных минимумов. Например, если оценка неизвестного параметра модели регрессии будет немного изменена, то значение функция потерь практически не изменится, но существует вероятность того, что ошибочное значение оцениваемого параметра модели регрессии даст в результате ощутимое уменьшение функции ошибок. Такое явление называется локальным минимумом. Следствием локальных минимумов являются неоправданно завышенные или заниженные оценки неизвестных параметров модели регрессии. Избежать попадания в локальный минимум можно путём повторения процедуры оценивания неизвестных параметров модели регрессии с изменёнными начальными условиями (шагом, ограничением оцениваемых параметров и т. д.). При достижении функцией ошибок глобального минимума, оценки неизвестных коэффициентов модели регрессии считаются оптимальными. К основным методам минимизации функции ошибок относятся: Квази-ньютоновский метод. Как вы, наверное, помните, угловой коэффициент - тангенс угла наклона графика функции в конкретной точке равен производной этой функции (в этой точке), а скорость его изменения в выбранной точке равна второй производной функции в этой точке. Квази-ньютоновский метод вычисляет значения функции в различных точках для оценивания первой и второй производной, используя эти данные для определения направления изменения параметров и минимизации функции потерь. Симплекс-метод. Этот алгоритм не использует производные функции потерь. Вместо этого, при каждой итерации функция оценивается в m+1 точках m -мерного пространства. Например, на плоскости (т.е., при оценивании двух параметров) программа будет вычислять значение функции потерь в трех точках в окрестности текущего минимума. Эти три точки определяют треугольник; в многомерном пространстве. Получаемая фигура называется симплекс. Интуитивно понятно, что в двумерном пространстве три точки позволяют выбрать “в каком направлении двигаться”, т.е., в каком направлении на плоскости менять параметры для минимизации функции. Похожие принципы применимы в многомерном параметрическом пространстве; т.е., симплекс будет постепенно “смещаться вниз по склону”, в сторону минимизации функции потерь; если же текущий шаг окажется слишком большим для определения точного направления спуска, (т.е., симплекс слишком большой), процедура произведет уменьшение симплекса и продолжит вычисления. Дополнительное преимущество симплекс-метода в том, что при нахождении минимума симплекс снова увеличивается для проверки: не является ли этот минимум локальным. Таким образом, симплекс движется по поверхности по направлению к минимуму функции подобно простому, одноклеточному, организму, уменьшаясь и увеличиваясь при обнаружении локальных минимумов и “гребней”. Метод Розенброка. Даже если все остальные методы не сработали, метод Розенброка часто приводит к правильному результату. Этот метод вращает пространство параметров, располагая одну ось вдоль “гребня” поверхности (этот метод также называется метод вращения координат), при этом все другие остаются ортогональными выбранной оси. Если поверхность графика функции потерь имеет одну вершину и различимые “гребни” в направлении минимума функции потерь, этот метод приводит к очень точным значениям параметров, минимизирующим функцию потерь. Однако следует отметить, что этот поисковый алгоритм остановится преждевременно, если на область значений параметров наложены несколько ограничений (отражающихся в штрафном значении; см. выше), которые пересекаются, приводя к обрыванию “гребня”.
|



 на z, получим линейное уравнение регрессии y = a + bz +ε оценка параметров которого может быть дана МНК.
на z, получим линейное уравнение регрессии y = a + bz +ε оценка параметров которого может быть дана МНК.
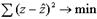
 ,
,





