При нарушении гомоскедастичности и наличии автокорреляции ошибок рекомендуетсятрадиционный МНК заменять
обобщенным методом. Обобщенный МНКприменяется к преобразованным данным и позволяет получать оценки, которыеобладают не только свойством несмещенности, но и имеют меньшие выборочныедисперсии. Обобщенный МНК для корректировки гетерос-ти. В общем виде дляуравнения y
i=a+bx
i+
e i при

где K
i – коэф-т пропор-ти. Модель примет вид: y
i=
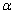
+

x
i+
 e i
e i. В ней остаточные величины гетероскедастичны. Предполагая вних отсутствие автокорреляции, можно перейти к уравнению с гомоскедастичнымиостатками, поделив все переменные, зафиксированные в ходе i-го наблюдения на

. Тогда дисперсия остатков будет величиной постоянной. От регрессии у по хмы перейдем к регрессии на новых переменных:
y/ 
и
х/ 
. Уравнение регрессии примет вид:

. По отношению к обычной регрессии уравнение с новыми, преобразованнымипеременными представляет собой
взвешенную регрессию, в которойпеременные
у и
х взяты с весами
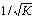
. Коэф-т регрессии b можно определить как

Как видим, при использовании обобщенного МНК с целью корректировкигетероскедастичности коэффициент регрессии
b представляет собойвзвешенную величину по отношению к обычному МНК с весами 1/К.Аналогичный подходвозможен не только для уравнения парной, но и для множественной регрессии.Модель примет вид:
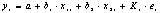
. Модель с преобразованными переменными составит

. Это уравнение несодер-т свобод-го члена, применяя обычный МНК получим:

Применение в этом случае обобщенного МНК приводит к тому, что наблюдения сменьшими значениями преобразованных переменных х/К имеют при определениипараметров регрессии относительно больший вес, чем с первоначальнымипеременными.
 где Ki – коэф-т пропор-ти. Модель примет вид: yi=
где Ki – коэф-т пропор-ти. Модель примет вид: yi= 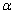 +
+  xi+
xi+  e i. В ней остаточные величины гетероскедастичны. Предполагая вних отсутствие автокорреляции, можно перейти к уравнению с гомоскедастичнымиостатками, поделив все переменные, зафиксированные в ходе i-го наблюдения на
e i. В ней остаточные величины гетероскедастичны. Предполагая вних отсутствие автокорреляции, можно перейти к уравнению с гомоскедастичнымиостатками, поделив все переменные, зафиксированные в ходе i-го наблюдения на  . Тогда дисперсия остатков будет величиной постоянной. От регрессии у по хмы перейдем к регрессии на новых переменных: y/
. Тогда дисперсия остатков будет величиной постоянной. От регрессии у по хмы перейдем к регрессии на новых переменных: y/  и х/
и х/  . Уравнение регрессии примет вид:
. Уравнение регрессии примет вид:  . По отношению к обычной регрессии уравнение с новыми, преобразованнымипеременными представляет собой взвешенную регрессию, в которойпеременные у и х взяты с весами
. По отношению к обычной регрессии уравнение с новыми, преобразованнымипеременными представляет собой взвешенную регрессию, в которойпеременные у и х взяты с весами 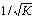 . Коэф-т регрессии b можно определить как
. Коэф-т регрессии b можно определить как  Как видим, при использовании обобщенного МНК с целью корректировкигетероскедастичности коэффициент регрессии b представляет собойвзвешенную величину по отношению к обычному МНК с весами 1/К.Аналогичный подходвозможен не только для уравнения парной, но и для множественной регрессии.Модель примет вид:
Как видим, при использовании обобщенного МНК с целью корректировкигетероскедастичности коэффициент регрессии b представляет собойвзвешенную величину по отношению к обычному МНК с весами 1/К.Аналогичный подходвозможен не только для уравнения парной, но и для множественной регрессии.Модель примет вид: 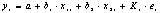 . Модель с преобразованными переменными составит
. Модель с преобразованными переменными составит  . Это уравнение несодер-т свобод-го члена, применяя обычный МНК получим:
. Это уравнение несодер-т свобод-го члена, применяя обычный МНК получим:  Применение в этом случае обобщенного МНК приводит к тому, что наблюдения сменьшими значениями преобразованных переменных х/К имеют при определениипараметров регрессии относительно больший вес, чем с первоначальнымипеременными.
Применение в этом случае обобщенного МНК приводит к тому, что наблюдения сменьшими значениями преобразованных переменных х/К имеют при определениипараметров регрессии относительно больший вес, чем с первоначальнымипеременными. 



