Выполнение предпосылки МНК о случайном характере остатков модели.
Метод наименьших квадратов дает «хорошие» оценки коэффициентов регрессии при выполнении некоторых условий. Эти условия касаются случайные компоненты Для однофакторной модели это след.условия: 1) В многофакторной модели добавляются следующие условия: 4) это независимость факторов между собой т.е.
Условие:
Метод наименьших квадратов при отсутствии ошибок в расчетах всегда дает выражение данного условия. 2)
Если остатки имеют постоянную дисперсию, то они называются гомаскедастичными, являются называются гомоскедастичностью. Если остатки непостоянны, то они называются гетероскедостичными, а явление называется гетероскедастичностью. Гетероскедастичность приводит к тому, что коэффициенты регрессии не представляют собой лучшие оценки или не являются оценками с наименьшей дисперсией. Следовательно они не являются «хорошими» коэффициентами. Непостоянство дисперсий часто встречается в моделях нестационарной экономики(Рссия), когда в качестве исходных данных используется временные ряды стоимостных показателей. В пространстве выборках гетероскедастичность встречается когда анализируемые объекты не однородны по своему масштабу. Гетероскедичность ведет к тому что стандартные ошибки будут смещенными, решение о наличии гетероскедичности принимается на основе общей процедуры проверки гипотез. Один из критериев F-критерий
Данный F-критерий имеет F – распределение со степенями свободы n1=n/2-k, n2=n/2-k При этих степенях свободы находим Fтабл, сравнивая Fрасч с Fтабл 1) если Fрасч попадает в интервал 2) если Fр >Fт, то дисперсия уменьшается 3) если Fр <1/Fт то дисперсия увеличивается
|

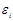 .
.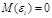 2)
2)  3)
3) 
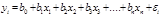
 1)
1) 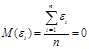
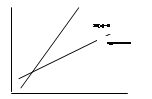
 Нарушение условия 2) когда дисперсия случайной компоненты не является постоянной, можно на графике изобразить следующим образом:
Нарушение условия 2) когда дисперсия случайной компоненты не является постоянной, можно на графике изобразить следующим образом:

 то дисперсия пост-а
то дисперсия пост-а


