Классы эконометрических моделей.(с 10)
Главным инструментом эконометрического исследования является модель. Выделяют три основных класса эконометрических моделей: 1. Моделью временных рядов называется зависимость результативной переменной от переменной времени или переменных, относящихся к другим моментам времени. К моделям временных рядов, характеризующих зависимость результативной переменной от времени, относятся: а) модель зависимости результативной переменной от трендовой компоненты или модель тренда; б) модель зависимости результативной переменной от сезонной компоненты или модель сезонности; в) модель зависимости результативной переменной от трендовой и сезонной компонент или модель тренда и сезонности. К моделям временных рядов, характеризующих зависимость результативной переменной от переменных, датированных другими моментами времени, относятся: а) модели с распределённым лагом, объясняющие вариацию результативной переменной в зависимости от предыдущих значений факторных переменных; б) модели авторегрессии, объясняющие вариацию результативной переменной в зависимости от предыдущих значений результативных переменных; в) модели ожидания, объясняющие вариацию результативной переменной в зависимости от будущих значений факторных или результативных переменных. 2) Моделью регрессии с одним уравнением называется зависимость результативной переменной, обозначаемой как у, от факторных переменных, обозначаемых как х1,х2,…,хn. Данную зависимость можно представить в виде функции регрессии или модели регрессии: y=f(x,β)=f(х1,х2,…,хn, β1…βk) где β1…βk – параметры модели регрессии. Можно выделить две основных классификации моделей регрессии: а) классификация моделей регрессии на парные и множественные регрессии в зависимости от числа факторных переменных; б) классификация моделей регрессии на линейные и нелинейные регрессии в зависимости от вида функции f(x,β). В качестве примеров моделей регрессии с одним уравнением можно привести следующие модели: а) производственная функция вида Q=f(L,K), выражающая зависимость объёма производства определённого товара (Q) от производственных факторов – от затрат капитала (К) и затрат труда (L); б) функция цены Р=f(Q,Pk), характеризующая зависимость цены определённого товара (Р) от объема поставки (Q) и от цен конкурирующих товаров (Pk); в) функция спроса Qd=f(P,Pk,I), характеризующая зависимость величины спроса на определённый товар (Р) от цены данного товара (Р), от цен товаров-конкурентов (Pk) и от реальных доходов потребителей (I). 3) Системы одновременных уравнений могут включать в себя тождества и регрессионные уравнения, в каждое из которых могут входить не только факторные переменные, но и результативные переменные из других уравнений системы. Примером системы одновременных уравнений является модель спроса и предложения, в которую входит три уравнения: а) уравнение предложения: =а0+а1*Рt+a2*Pt-1; б) уравнение спроса: =b0+b1* Рt+b2*It; в) тождество равновесия: QSt = Qdt, где QSt – предложение товара в момент времени t; Qdt – спрос на товар в момент времени t; Рt – цена товара в момент времени t; Pt-1 – цена товара предшествующий момент времени (t-1);It– доход потребителей в момент времени.
Основные понятия регрессионного анализа.(с34-36) Регрессионный анализ — метод моделирования измеряемых данных и исследования их свойств. Данные состоят из пар значений зависимой переменной (переменной отклика) и независимой переменной (объясняющей переменной). Регрессионная модель есть функция независимой переменной и параметров с добавленной случайной переменной. Параметры модели настраиваются таким образом, что модель наилучшим образом приближает данные. Критерием качества приближения (целевой функцией) обычно является среднеквадратичная ошибка: сумма квадратов разности значений модели и зависимой переменной для всех значений независимой переменной в качестве аргумента. Регрессионный анализ — разделматематической статистики и машинного обучения. Предполагается, что зависимая переменная есть сумма значений некоторой модели и случайной величины. Относительно характера распределения этой величины делаются предположения, называемые гипотезой порождения данных. Для подтверждения или опровержения этой гипотезы выполняются статистические тесты, называемые анализом остатков. При этом предполагается, что независимая переменная не содержит ошибок. Регрессионный анализ используется для прогноза, анализа временных рядов,тестирования гипотез и выявления скрытых взаимосвязей в данных. В статистической литературе различают регрессию с участием одной свободной переменной и с несколькими свободными переменными — одномерную и многомерную регрессию. Предполагается, что мы используем несколько свободных переменных, то есть, свободная переменная — вектор Различают параметрическую и непараметрическую регрессию. Строгую границу между этими двумя типами регрессий провести сложно. Сейчас нет существует общепринятого критерия отличия одного типа моделей от другого. Например, считается, что линейные модели являются параметрическими, а модели, включающие усреднение зависимой переменной по пространству свободной переменной —непараметрическими. Пример параметрической регресионной модели: линейный предиктор, многослойный персептрон. Примеры смешанной регрессионной модели: функции радиального базиса. Непараметрическая модель — скользящее усреднение в окне некоторой ширины. В целом, непараметрическая регрессия отличается от параметрической тем, что зависимая переменная зависит не от одного значения свободной переменной, а от некоторой заданной окрестности этого значения.
|

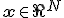 . В частных случаях, когда свободная переменная является скаляром, она будет обозначаться
. В частных случаях, когда свободная переменная является скаляром, она будет обозначаться  . Различают линейную и нелинейную регрессию. Если регрессионную модель не является линейной комбинацией функций от параметров, то говорят о нелинейной регрессии. При этом модель может быть произвольной суперпозицией функций
. Различают линейную и нелинейную регрессию. Если регрессионную модель не является линейной комбинацией функций от параметров, то говорят о нелинейной регрессии. При этом модель может быть произвольной суперпозицией функций 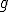 из некоторого набора. Нелинейными моделями являются, экспоненциальные, тригонометрические и другие (например, радиальные базисные функции или персептрон Розенблатта), полагающие зависимость между параметрами и зависимой переменной нелинейной.
из некоторого набора. Нелинейными моделями являются, экспоненциальные, тригонометрические и другие (например, радиальные базисные функции или персептрон Розенблатта), полагающие зависимость между параметрами и зависимой переменной нелинейной.


