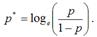Логит, пробит и экстрим модели.

Модель бинарного выбора называется пробит-моделью или пробит-регрессией (probit regression), если она удовлетворяет двум условиям:

1) остатки модели бинарного выбора εi являются случайными нормально распределёнными величинами;

2) функция распределения вероятностей является нормальной вероятностной функцией.

Пробит-регрессия может быть представлена с помощью выражения:

NP(yi)=NP(β0+β1x1i+…+βkxki),

где NP – это нормальная вероятность (normal probability).

Модель бинарного выбора называется логит-моделью или логит-регрессией (logit regression), если случайные остатки εi подчиняются логистическому закону распределения.

Логит-регрессия может быть представлена с помощью выражения:

Данная модель логит-регрессии характеризуется тем, что при любых значениях факторных переменных и коэффициентов регрессии, значения результативной переменной yi будут всегда лежать в интервале [0;+1].

Обобщённый вид модели логит-регрессии:

Достоинством данной модели является то, что результативная переменная yi может произвольно меняться внутри заданного числового интервала (не только от нуля до плюс единицы).

Логит-регрессия относится к классу функций, которые можно привести к линейному виду. Это осуществляется с помощью преобразования, носящего название логистического или логит преобразования, которое можно проиллюстрировать на примере преобразования обычной вероятности р:

Качество построенной логит-регрессии или пробит-регрессии характеризуется с помощью псевдо коэффициента детерминации, который рассчитывается по формуле:

Если значение данного коэффициента близко к единице, то модель регрессии считается адекватной реальным данным.