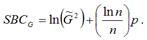Селекция моделей бинарного выбора с помощью информационных критериев Акайке и Шварца

Основными показателями качества модели авторегрессии и проинтегрированного скользящего среднего являются критерий Акайка и байесовский критерий Шварца. Данные критерии аналогичны критерию максимума скорректированного множественного коэффициента детерминации R2 или минимума дисперсии случайной ошибки модели G2.

Информационный критерий Акайка (Akaike information criterion – AIC) используется для выбора наилучшей модели для временного ряда yt из некоторого множества моделей.

Предположим, что с помощью метода максимального правдоподобия была получена оценка вектора неизвестных параметров модели φ. Обозначим через максимальное значение логарифмической функции правдоподобия эконометрической модели.Тогда критерий Акайка можно будет представить в виде:

где h – размерность вектора неизвестных параметров модели φ.

Для линейной или нелинейной модели регрессии, включающей только одно уравнение, критерий Акайка может быть преобразован к виду: где n – объём выборочной совокупности;

– оценка максимального правдоподобия дисперсии остатков et модели регрессии.

Оба варианта критерия Акайка дают одинаковый результат, но в первом случае выбирается модель с наибольшим значением критерия, а во втором случае – с наименьшим значением критерия.

Байесовский критерий Шварца (Schwarz Bayesian criterion – SBC) также используется для выбора наилучшей модели временного ряда из некоторого множества моделей.

Байесовский критерий Шварца для временных рядов можно представить в виде:

Байесовский критерий Шварца для моделей регрессии можно представить в виде:

По первому варианту расчёта критерия Байесовского критерий Шварца SBC выбирается та модель, для которой значение SBCt является наибольшим. При втором варианте выбирается та модель, для которой значение SBCG является наименьшим.

При проверке качества моделей результаты критериев Акайка и Шварца могут быть различны.