Проверка значимости уравнения бинарной регрессионной модели на основе теста отношения правдоподобия (LR-тест)
Проверку значимости уравнения регрессии производят на основе вычисления F- критерия Фишера: где m- число параметров в уравнении регрессии. Полученное значение — критерия Fpacч сравнивают с критическим (табличным) для принятого уровня значимости 0,05 или 0,01 и чисел степеней свободы ν1 = m — 1 и ν2 = n- m. Если оно окажется больше соответствующего табличного значения, то данное уравнение регрессии статистически значимо, т. е. доля вариации, обусловленная регрессией, намного превышает случайную ошибку. Принято считать, что уравнение регрессии пригодно для практического использования в том случае, если Fpacч > Fтабл не менее чем в 4 раза. Для оценки значимости коэффициентов регрессии при линейной зависимости у от x1 и x2 - (двух факторов) используют t-критерий Стьюдента при n-m-1 степенях свободы:
Значения оцениваемых a1, a2 , Если в уравнении все коэффициенты регрессии значимы, то данное уравнение признают окончательным и применяют в качестве модели изучаемого показателя для последующего анализа. Оценку значимости коэффициентов регрессии с помощью t Последовательный отсев несущественных факторов рассмотренным выше приемом (или последовательным включением новых факторов) составляет основу многошаговогорегрессионногоанализа. Проверим адекватность построенной двухфакторной модели производительности труда по F-критерию Фишера: Табличное значение F-критерия при доверительной вероятности 0.95, т. е. (1-0,05) при н1 = т - 1 = 2 - 1 = 1; н2= n Поскольку Fpacч > Fтабл уравнение регрессии Значимость a1 , a2 и
где-
Данная статистика, как и в общем случае использования метода максимального правдоподобия, позволяет тестировать статистическую значимость модели в целом. Если её значение достаточно большое (больше критического значения распределения
|

 (9.23)
(9.23)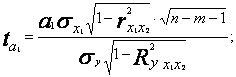 (9.24, a
(9.24, a (9.24, б)
(9.24, б) (9.25)
(9.25) берутся по модулю.
берутся по модулю.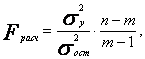

 = 81,03-0,41 x1+3,37 x2 следует признать адекватным.
= 81,03-0,41 x1+3,37 x2 следует признать адекватным.



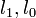 значения логарифмической функции правдоподобия оцененной модели и ограниченной модели, в которой
значения логарифмической функции правдоподобия оцененной модели и ограниченной модели, в которой  является константой (не зависит от факторов x, исключая константу из множества факторов).
является константой (не зависит от факторов x, исключая константу из множества факторов). где К -количество факторов (без константы) модели), то модель можно признать статистически значимой
где К -количество факторов (без константы) модели), то модель можно признать статистически значимой


