Задание. 1.Причини виникнення автокореляції в економетричних моделях
1.Причини виникнення автокореляції в економетричних моделях 1.1. Поняття автокореляції 1.2. Наслідки автокореляції залишків 2. Перевірка наявності автокореляції 2.1. Критерій Дарбіна –Уотсона 2.2. Критерій фон Неймана Автокореляція — це взаємозв'язок послідовних елементів часового чи просторового ряду даних. В економетричних моделях особливе значення має автокореляція залишків. Автокореляція залишків найчастіше спостерігається тоді, коли економетрична модель будується на основі часових рядів. Якщо існує кореляція між послідовними значеннями деякої незалежної змінної, то спостерігатиметься і кореляція послідовних значень залишків. Автокореляція може бути також наслідком помилкової специфікації економетричної моделі. Крім того, наявність автокореляції залишків може означати, що необхідно ввести до моделі нову незалежну змінну. У загальному випадку ми вводимо до моделі лише деякі з істотних змінних, а вплив змінних, які виключені з моделі, має позначитися на зміні залишків. Існування кореляції між послідовними значеннями виключеної з розгляду змінної не обов'язково має тягти за собою відповідну кореляцію залишків, бо вплив різних змінних може взаємно погашатися. Якщо кореляція послідовних значень виключених з моделі змінних спостерігається, то загроза виникнення автокореляції залишків стає реальністю. Проілюструємо проблему автокореляції залишків на прикладі економетричної моделі з двома змінними. Нехай
де ми припускаємо, що залишки u, задовольняють схему авторегресії першого порядку, тобто залежать тільки від залишків попереднього періоду. Специфікація моделі (1) має індекс t, що свідчить про її динамічний характер, тобто t — період часу, для якого будується така модель на основі динамічних (часових) рядів вихідних даних. Якщо знехтувати автокореляцією залишків і оцінити параметри моделі 1МНК, то матимемо такі три наслідки. 1. Оцінки параметрів моделі можуть бути незміщеними, але неефективними, тобто вибіркові дисперсії вектора оцінок А можуть бути невиправдано великими. 2.Оскільки вибіркові дисперсії обчислюються не за уточненими формулами, то статистичні критерії t - і F-статистики, які знайдено для лінійної моделі, практично не можуть бути використані в дисперсійному аналізі. 3.Неефективність оцінок параметрів економетричної моделі призводить, як правило, до неефективних прогнозів, тобто прогнозів з дуже великою вибірковою дисперсією. Для перевірки наявності автокореляції залишків найчастіше застосовується критерій Дарбіна — Уотсона (DW):
Він може приймати значення з проміжку [0, 4]: DW є [0, 4]. Якщо залишки ut є випадковими величинами, нормально розподіленими, а не автокорельованими, то значення DW містяться поблизу 2. При додатній автокореляції DW<2, при від'ємній — DW > 2. Фактичні значення критерію порівнюються з критичними (табличними) при різному числі спостережень п і числі незалежних змінних т для вибраного рівня значущості а. Табличні значення мають нижню межу DW1 і верхню — DW2. Коли DWфакт < DW1, то залишки мають автокореляцію. Якщо DWфакт > DW2, то приймається гіпотеза про відсутність автокореляції. Коли DW1 <DW< DW2, то конкретних висновків зробити не можна: необхідно далі проводити дослідження, беручи більшу сукупність спостережень. Зауважимо, що цей критерій призначений для малих вибіркових сукупностей. Наведені співвідношення показують, що існують області, в яких застосування критерію Дарбіна - Уотсона не може дати певних результатів, про що вже зазначалося. Верхні та нижні межі критерію DW визначають межі цієї області для різних розмірів вибірки, заданого числа пояснювальних змінних та певного рівня значущості. Для виявлення автокореляції залишків використовується також критерій фон Неймана:
Звідси Приклад. За допомогою двох взаємопов'язаних часових рядів про роздрібний товарообіг та доходи населення побудувати економетричну модель, що характеризує залежність роздрібного товарообігу від доходу. Вихідні дані наведено в табл. 1.
1. Вихідні дані
Розв'язання 1. Ідентифікуємо змінні моделі:
звідси
де 2. Специфікуємо економетричну модель у лінійній формі:
де и — скаляр; у — вектор; х — матриця. 3. Визначимо оцінки параметрів моделі
де X' — матриця, транспонована до X.
Економетрична модель має вигляд:
4. Знайдемо розрахункові значення роздрібного товарообігу на основі моделі Знайдемо оцінку критерію Дарбіна — Уотсона:
Порівняємо значення критерію DW з табличним для α = 0,05 і п= 10. Критичні значення критерію DW у цьому разі такі: D W1| = 0,879 — нижня межа; DW2 = 1,320 — верхня межа. Оскільки критерій DWфакт < DW1, то можна стверджувати, що залишки uмають додатну автокореляцію. Наявність чи відсутність автокореляції залишків можна також визначити згідно з критерієм фон Неймана. 2.Розрахункові значення для знаходження критерію Дарбіна - Уотсона
Критерій фон Неймана
Зміст
Задание Разновидность идеализма, провозглашающая независимость идеального начала, не только от материи, но и от сознания человека: 1. субъективный 2. диалектический 3. объективный 4. последовательный 5. непоследовательный
|

 , (1)
, (1) (2)
(2)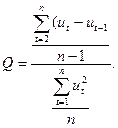 (3)
(3) при
при  . Фактичне значення критерію фон Неймана порівнюється з табличним для вибраного рівня значущості і заданого числа спостережень. Якщо
. Фактичне значення критерію фон Неймана порівнюється з табличним для вибраного рівня значущості і заданого числа спостережень. Якщо  , то існує додатна автокореляція.
, то існує додатна автокореляція. — роздрібний товарообіг у період t, залежна змінна;
— роздрібний товарообіг у період t, залежна змінна; — дохід у період t, пояснювальна змінна;
— дохід у період t, пояснювальна змінна;
 − стохастична складова, залишки.
− стохастична складова, залишки.
 ,
, 
 за методом найменших квадратів, припускаючи що залишки
за методом найменших квадратів, припускаючи що залишки 
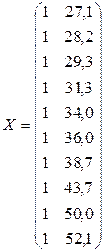

 .
.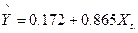 і визначимо залишки и, (табл. 2).
і визначимо залишки и, (табл. 2). .
.

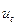
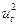



 . Це значення порівнюється з табличним; Qтабл =1,18 при п = 10 і рівні значущості α = 0,05. Оскільки Qфакт < Qтабл, то існує додатна автокореляція залишків.
. Це значення порівнюється з табличним; Qтабл =1,18 при п = 10 і рівні значущості α = 0,05. Оскільки Qфакт < Qтабл, то існує додатна автокореляція залишків.


