Расчет надежности восстанавливаемых систем
Процесс функционирования восстанавливаемой нерезервированной системы может быть отражен графом состояний (рис. 1.4.1).
1. Коэффициент готовности:
где
Поэтому Учитывая, что
Статистически
где
2. Коэффициент простоя:
где
Статистически, по аналогии с (1.4.3),
, (1.4.8)
т.к.
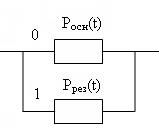
Рассмотрим восстанавливаемую резервированную систему, в которой используется постоянное общее резервирование с кратностью резервирования m, равной единице (дублированную систему). Структурная схема надежности (ССН) такой системы будет иметь следующий вид:
При этом будем считать, что основная и резервная системы являются одинаковыми и равнонадежными, то есть
Росн(t)= Ррез(t)= Р(t).
Причем надежность этих систем имеет показательный закон, то есть:
Состояния резервированной восстанавливаемой системы отображаются соответствующим графом состояний. На рис. 1.4.3 изображен граф состояний рассматриваемой системы.
Рис. 1.4.3
Состояния системы на графе означают: G 0 – основная и резервная система работоспособны; G 1 – одна из систем (основная или резервная) отказала, а вторая работоспособна; G 2 – основная и резервная системы отказали; резервированная система неработоспособна. Вероятности нахождения резервированной системы в соответствующих состояниях обозначены следующим образом: Р0(t), Р1(t), Р2(t). Переход системы из одного состояния в другое происходит под воздействием потоков отказов с интенсивностью λ; и потоков восстановлений с интенсивностью μ;. Дуге, идущей из состояния G 0 в состояние G 1, приписано значение интенсивности отказов, равное 2λ;, так как в состоянии G 0 работают две системы и отказать может или основная система с интенсивностью λ;, или резервная система с такой же интенсивностью λ;. Дуге, идущей из состояния G 2 в состояние G 1, приписано значение интенсивности восстановления 2μ;, что означает условие неограниченного восстановления: одновременно могут восстанавливаться обе отказавшие системы (и основная, и резервная). В этом случае одновременно работают две бригады ремонтников. В общем случае вид графа состояний резервированной восстанавливаемой системы зависит от следующих факторов: 1) от способа структурного резервирования; 2) от кратности резервирования m; 3) от режима восстановления (неограниченное или ограниченное). Процесс функционирования восстанавливаемой системы является марковским случайным процессом с дискретными состояниями, то есть дискретным случайным процессом. Случайный процесс называется дискретным, если его состояния можно пронумеровать и переход из состояния в состояние происходит скачком. Случайный дискретный процесс называется марковским, если для любого момента времени t вероятности всех состояний системы в будущем зависят только от ее состояния в настоящем и не зависят от того, когда и как эта система перешла в это состояние. Если потоки отказов и восстановлений, переводящие систему из состояния в состояние являются ординарными и без последствия, то есть пуассоновскими, то случайный процесс есть марковский. Марковский случайный процесс описывается системой линейных дифференциальных уравнений, которую предложил академик Колмогоров А.Н.. Дифференциальные уравнения для любой восстанавливаемой резервированной системы по известному графу составляются по следующим правилам: 1) число дифференциальных уравнений равно числу состояний графа; 2) производная вероятности нахождения системы в каком-либо состоянии равна алгебраической сумме такого числа слагаемых, сколько стрелок связано с этим состоянием; 3) каждое слагаемое равно произведению интенсивности потока событий (отказов или восстановлений), переводящей систему по данной стрелке, на вероятность того состояния, из которого исходит стрелка; 4) слагаемое имеет знак «–», если стрелка исходит из данного состояния; и знак «+», если стрелка направлена в данное состояние. Запишем систему дифференциальных уравнений для графа, представленного на рис. 1.4.3:
(1.4.9)
Данная система уравнений (1.4.9) решается или численными методами, или с использованием преобразований Лапласа. Переменными в системе уравнений (1.4.9), которые необходимо найти, являются вероятности нахождения системы в состояниях Систему дифференциальных уравнений (1.4.9) можно привести к системе линейных алгебраических уравнений, если воспользоваться предельной теоремой Маркова А.А.: Если все интенсивности потоков событий (λ и μ) постоянны, а граф состояний таков, что из каждого состояния можно перейти в каждое другое состояние за конечное число шагов, то предельные вероятности состояний существуют и не зависят от начального состояния системы. В соответствии с этой теоремой при
Немецкий математик Гаусс доказал, что система линейных уравнений тогда имеет решение, когда все уравнения, входящие в систему, являются линейно независимыми. Это означает, что ни одно из уравнений системы (3.34) не может являться суммой каких-то других уравнений, входящих в эту систему. Полученная система уравнений (1.4.10) является линейно зависимой. Например, если сложим первое и второе уравнения, то с точностью до знаков получим третье уравнение; сумма второго и третьего даст первое уравнение; сумма первого и третьего даст второе уравнение. В связи с этим исключим из системы уравнений (1.4.10) второе уравнение и добавим в систему (1.4.10) нормировочное уравнение вида: Р 0(t)+ Р 1(t)+ Р 2(t)=1. Тогда система линейно независимых уравнений примет вид:
 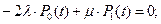
Р 0(t)+ Р 1(t)+ Р 2(t)=1.
где i = 0, 1, 2; D – определитель, составленный из коэффициентов системы уравнений (3.35) при переменных P i (t); Di – определитель, в котором i -й столбец в определителе D заменяется столбцом свободных членов. Безотказными состояниями в рассматриваемой системе являются G0 и G1; состояние отказа – G2. Для восстанавливаемых резервированных систем показателями надежности являются комплексные показатели, то есть коэффициенты готовности КГ и простоя КП. После вычисления вероятностей Pi(t) по формуле (1.4.12) определяют численные значения коэффициента готовности
КГ = Р0(t)+ Р1(t), который оценивает вероятность нахождения системы в работоспособном состоянии, и коэффициента простоя
КП = Р2(t), или КП =1 – КГ,
определяющего вероятность нахождения системы в режиме восстановления. На последнем этапе расчета осуществляется сравнение вычисленного значения коэффициента готовности с заданным значением в соответствие с неравенством:
Если неравенство (1.4.13) не выполняется, то увеличивают кратность резервирования m на единицу и расчет надежности проводится повторно. Методика решения задачи расчета надежности восстанавливаемых резервированных систем следующая. В качестве исходных данных при расчете задаются: 1) способ резервирования и кратность резервирования m; 2) заданное значение коэффициента готовности КГзад; 3) способ восстановления работоспособного состояния системы (ограниченное или неограниченное восстановление). Требуется вычислить значение коэффициента готовности КГ и сравнить его с заданным значением. Решение данной задачи производится в следующей последовательности: 1) изображаем ССН и граф состояний системы; 2) записываем систему линейных алгебраических уравнений вида (1.4.10); 3) приводим систему уравнений (1.4.10) к системе линейных независимых уравнений (1.4.11); 4) составляем определители D и Di (i =0, 1, 2); 5) вычисляем вероятности нахождения системы в i-х состояниях Pi(t) по формуле (1.4.12); 6) вычисляем коэффициент готовности КГ как сумму вероятностей нахождения системы в работоспособных состояниях; 7) производим сравнение вычисленного значения КГ с заданным значением КГзад . При невыполнении неравенства (1.4.13) кратность резервирования m увеличиваем на единицу и повторяем вычисление коэффициента КГ .
|


 , (1.4.1)
, (1.4.1)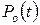 – вероятность нахождения системы в состоянии
– вероятность нахождения системы в состоянии 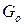 ;
; – средняя наработка на отказ восстанавливаемой системы. Она численно равна средней наработке до отказа То для одного интервала безотказной работы, т.е.
– средняя наработка на отказ восстанавливаемой системы. Она численно равна средней наработке до отказа То для одного интервала безотказной работы, т.е. 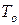 . Тогда
. Тогда 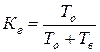 ;
;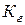 – характеризует среднюю относительную долю времени нахождения системы в работоспособном состоянии.
– характеризует среднюю относительную долю времени нахождения системы в работоспособном состоянии.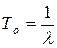 , а
, а 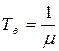 , получим:
, получим: . (1.4.2)
. (1.4.2)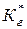 определяется:
определяется: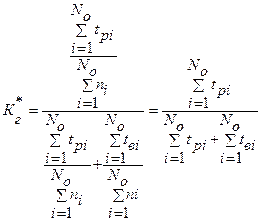 , (1.4.3)
, (1.4.3)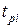 – суммарное время безотказной работы i – го образца;
– суммарное время безотказной работы i – го образца; – суммарное число отказов i – го образца.
– суммарное число отказов i – го образца.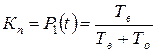 , (1.4.5)
, (1.4.5)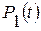 – вероятность нахождения системы в состоянии
– вероятность нахождения системы в состоянии 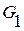 .
. – характеризует относительную долю времени нахождения системы в режиме восстановления.
– характеризует относительную долю времени нахождения системы в режиме восстановления. . (1.4.6)
. (1.4.6)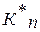 равен:
равен: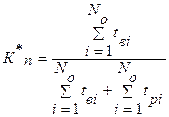 , (1.4.7)
, (1.4.7)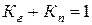
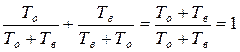 .
.
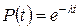 – вероятность безотказной работы основной или резервной системы.
– вероятность безотказной работы основной или резервной системы.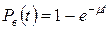 – вероятность восстановления работоспособного состояния основной или резервной системы.
– вероятность восстановления работоспособного состояния основной или резервной системы.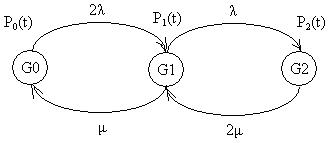

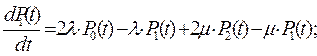
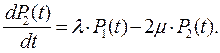
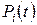 (i =0, 1, 2).
(i =0, 1, 2). вероятности нахождения системы в безотказных состояниях
вероятности нахождения системы в безотказных состояниях 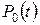 ,
, 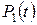 будут равны нулю, то есть
будут равны нулю, то есть 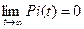 (i=0, 1), а вероятность нахождения системы в состоянии отказа
(i=0, 1), а вероятность нахождения системы в состоянии отказа 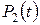 будет равна единице, то есть
будет равна единице, то есть 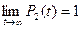 . Поэтому производные в левых частях уравнений системы (1.4.9) можно приравнять к нулю. Тогда получим систему линейных алгебраических уравнений следующего вида:
. Поэтому производные в левых частях уравнений системы (1.4.9) можно приравнять к нулю. Тогда получим систему линейных алгебраических уравнений следующего вида:

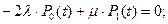
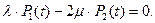
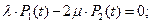
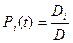 ,
,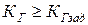 (1.4.13)
(1.4.13)


