Решение. 1. Чертим структурную схему надежности восстанавливаемой резервированной системы (рис1. Чертим структурную схему надежности восстанавливаемой резервированной системы (рис. 3.5)
Рис. 3.5
2. Чертим граф состояний системы (рис. 3.6)
Рис. 3.6
3. С использованием полученного графа состояний системы записываем систему линейных алгебраических уравнений по указанным в разделе 1 правилам (правилам составления дифференциальных уравнений Колмогорова А.Н.):
Полученная система уравнений является линейно зависимой. 4. Приводим данную систему уравнений к системе линейно независимых уравнений путем исключения второго уравнения и добавления нормировочного уравнения:
5. Используя полученную систему уравнений, составляем и вычисляем определители D и Di (i =0, 1, 2):
6. Вычисляем вероятности нахождения восстанавливаемой резервированной системы в соответствующих состояниях G0, G1, G2:
7. Вычисляем коэффициент готовности:
КГ = P0(t)+P1(t) =0,990000+0,009900=0,9999.
Вывод. Вычисленное значение коэффициента готовности превышает заданное значение (
Задача № 4 Для восстанавливающего органа (ВО) типа
Типовой пример. Для восстанавливающего органа (ВО) типа
|
;
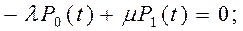
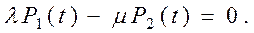
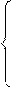
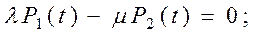
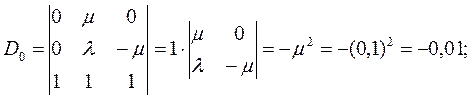
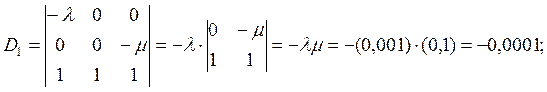
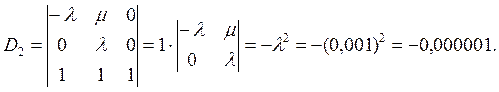
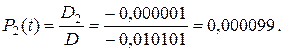
). Следовательно, кратность резервирования m =1 является достаточной.
(в соответствии с вариантом: номер варианта определяется двумя последними цифрами номера зачетной книжки студента) запишите логическую функцию (функцию алгебры логики) и постройте структурную схему на основе логических элементов «И», «ИЛИ». Определите количество отказов по «0» и «1», которое может корректировать восстанавливающий орган данного типа. Исходные данные: 
и 
, если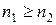 
или 
и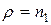 
, если 
> 
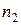, где n 1 – последняя цифра номера зачетной книжки (цифра 0 соответствует n1=10); n2 – предпоследняя цифра номера зачетной книжки (цифра 0 соответствует n2=10).
запишите логическую функцию (функцию алгебры логики) и постройте структурную схему на основе логических элементов «И», «ИЛИ». Определите количество отказов по «0» и «1», которое может корректировать восстанавливающий орган данного типа.
