Определённый интеграл. Формула Ньютона – Лейбница. Несобственные интегралы 1 – го и 2 – го типов. Вычисление площадей плоских фигур.
Занятие 28
Контрольная работа по вычислению интегралов (неопределённый, определённый, несобственный).
Занятие 29
Функции многих независимых переменных. Область определения. Предел и
непрерывность. Частные производные. Полное приращение и полный дифференциал первого порядка функции нескольких переменных.
Занятие 30
Дифференцирование сложной функции нескольких независимых переменных.
Производные и дифференциалы высших порядков. Линии и поверхности уровня. Производная функции по заданному направлению. Градиент функции.
Занятие 31
Экстремум функции нескольких независимых переменных. Наибольшее и наименьшее значения функции двух независимых переменных. Необходимые и достаточные условия экстремума.
Занятие 32
Дифференциальные уравнения первого порядка. Уравнения с разделяющимися переменными. Особые решения уравнения с разделяющимися переменными. Линейные дифференциальные уравнения 1-го порядка.
Занятие 33
Дифференциальные уравнения высших порядков, допускающие понижение порядка. Уравнения, содержащие только производную порядка n и независимую переменную: 
. Уравнения, не содержащие искомой функции: 
. Уравнения, не содержащие независимой переменной: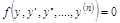 
.
Занятие 34
Линейные дифференциальные уравнения высших порядков. Линейные однородные уравнения с переменными коэффициентами. Линейные однородные дифференциальные уравнения с постоянными коэффициентами.
Занятие 35
Числовые ряды. Частичные суммы ряда. Сходимость ряда. Необходимый признак сходимости. Критерий Коши сходимости ряда. Ряды с положительными членами. Признаки сравнения. Признак Д'Аламбера и признак Коши сходимости рядов с положительными членами.
Занятие 36
Сходимость знакопеременных рядов. Абсолютная и условная сходимость. Признаки Лейбница и Абеля. Приближённое вычисление суммы ряда.
