Корректные и некорректные декомпозиции отношений. Теорема Хита (с доказательством). Минимально зависимые атрибуты.

Считаются правильными такие декомпозиции отношения, которые обратимы, т. е. имеется возможность собрать исходное отношение из декомпозированных отношений без потери информации. Такие декомпозиции называются декомпозициями без потерь.

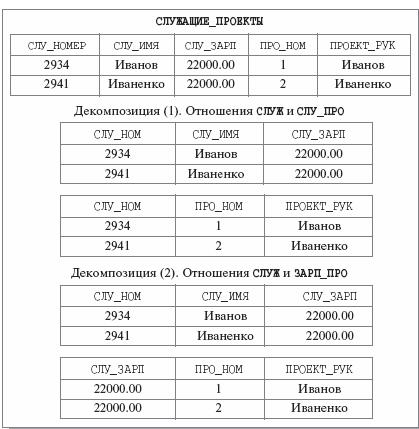
Рис. 7.3 Две возможные декомпозиции отношения СЛУЖАЩИЕ_ПРОЕКТЫ

Анализ рис. 7.3 показывает, что в случае декомпозиции (1) мы не потеряли информацию о служащих. Вторая декомпозиция не дает возможности получить данные о проекте служащего, поскольку Иванов и Иваненко получают одинаковую зарплату, следовательно, эта декомпозиция приводит к потере информации. Что же привело к тому, что одна декомпозиция является декомпозицией без потерь, а вторая – нет?

Схема этого отношения, естественно (поскольку соединение – естественное), совпадает со схемой отношения СЛУЖАЩИЕ_ПРОЕКТЫ, но в теле появились лишние кортежи, наличие которых и приводит к утрате исходной информации. Интуитивно понятно, что это происходит потому, что в отношении ЗАРП_ПРО отсутствуют функциональные зависимости СЛУ_ЗАРП->ПРО_НОМ и СЛУ_ЗАРП->ПРОЕКТ_РУК, но точнее причину потери информации в данном случае мы объясним несколько позже. Корректность же декомпозиции 1 следует из теоремы Хита:

Теорема Хита. Пусть задано отношение r {A, B, C} (A, B и C, в общем случае, являются составными атрибутами) и выполняется FD AB. Тогда r = (r PROJECT {A, B}) NATURAL JOIN (r PROJECT {A, C}).

Рис. 7.4. Результат естественного соединения отношений СЛУЖ и ЗАРП_ПРО

Доказательство.

Прежде всего, докажем, что в теле результата естественного соединения (обозначим этот результат через r1) содержатся все кортежи тела отношения r. Действительно, пусть кортеж {a, b, c} принадлежит r. Тогда по определению операции взятия проекции {a, b} принадлежит (r PROJECT {A, B}) и {a, с} принадлежит (r PROJECT {A, С}). Следовательно, {a, b, c} принадлежит r1. Теперь докажем, что в теле результата естественного соединения нет лишних кортежей, т. е. что если кортеж {a, b, c} принадлежит r1, то {a, b, c} принадлежит r. Если {a, b, c}- принадлежит r1, то существуют {a, b}, принадлежащее (r PROJECT {A, B}), и {a, с}, принадлежащее (r PROJECT {A, С}). Последнее условие может выполняться в том и только в том случае, когда существует кортеж {a, b*, c}= r. Но поскольку выполняется FD AB, то b = b* и, следовательно, {a, b, c} = {a, b*, c}. Конец доказательства.

Атрибут B минимально зависит от атрибута A, если выполняется минимальная слева FD AB.