Теориялық бөлім. Ұялы байланыс желісін жобалау кезінде жүйедегі трафикті (жүктеме қарқындылығын) бағалау қажет
Ұялы байланыс желісін жобалау кезінде жүйедегі трафикті (жүктеме қарқындылығын) бағалау қажет. Трафик негізінде ұядағы және барлық жүйедегі қызмет көрсетілетін абоненттер санын бағалауға болады. Сонымен, ұялы байланыс желісі, кез-келген телефондық байланыс жүйесі сияқты, кездейсоқ шақырулар ағымы, оларға қызмет көрсетудің кездейсоқ ұзақтылығы және нақтылы физикалық радиоарналар сандарымен сипатталатын жаппай қызмет көрсету жүйе мысалы болып табылады. Трафиктің математикалық модельдерін құру үшін келесі негізгі шамалар қолданылады: - шақырулар түсудің орташа жиілігі (λ), уақыт аралығында түсетін шақырулар саны ([λ] = шақыру/сағат, шақыру/секунда); - бір шақыруға қызмет көрсету ұзақтылығының орташа мәні (бір сөйлесудің орташа ұзақтылығы) (T), уақыт бірліктермен өлшенеді; - орташа жүктеме қарқындылығы
А = (λ)·(Т), (Эрл). (5.1)
Мысал қарастырайық. Егер шақырулар түсудің орташа жиілігі (λ) = 20 шақыру/сағат, бір шақыруға қызмет көрсетудің орташа ұзақтылығы (T) = 0,2 сағат, онда трафиктің орташа қарқындылығы А = 200,2 = 4 Эрл, яғни орташа жүктеме қарқындылығы 4 шақыруларға тең. Орташа трафик шамасын А байланыс жүйесінің ең жоғары жүктеме түсу уақыты үшін есептеледі. Шақырулардың ықтималдық сипаттамаларын анықтау Шақырулар түсуі және қызмет көрсету уақыты Т(t) кездейсоқ шамалар болып табылады. Ықтималдық теориясы үш факторлар арасындағы – жүктеме, арналар саны және қызмет көрсету сапасы арасындағы қатынастар шығаруға мүмкіндік береді. Шақырулар түсу ықтималдығы Пуассон таралуы арқылы сипатталады. Пуассон таралуы бойынша уақыт аралығында t k-шақырулар (дискретті кездейсоқ шама) түсуді сипаттайды:
егер [(λ) t] > 0, k ≥ 0. Уақыт интервалында t шақырулардың орташа саны:
Осы интервалда шақырулардың дисперсия саны:
мұндағы (λ) – шақырулар түсудің орташа жиілігі. 16-суретте (λ)t = 4 теңдесу үшін Пуассон таралуы көрсетілген, шақырулар түсудің максималды ықтималдығы k = 4 аймағында байқалады, яғни t уақытта 4 шақыру. Бір шақыруға қызмет көрсету ұзақтығы (байланыс арнасының қолдану ұзақтылығы) үзіліссіз кездейсоқ шама τ(t) болып табылады, ықтималдықтар таралу тығыздығы экспонента заңы арқылы көрсетіледі:
Осы шамаға орташа мәні (математикалық күтуі) және дисперсия сәйкес келеді: τ = (Е), ∆τ = (Т)2, яғни орташа мәні бір шақыруға қызмет көрсету ұзақтылығына (Т) сәйкес.
16 – сурет. Шақырулар түсу ықтималдылықтардың Пуассон таралуы
17 - суретте ω(τ) тәуелділіктер (Т) = 0,3 (график 1) және (Т) = 0,5 (график 2) үшін көрсетілген.
17 – сурет. Әр түрлі арнаның қолдану ұзақтылығы Т үшін ықтималдықтар таралу тығыздығы өзгерудің экспоненциалды заңы
Трафиктің математикалық модельдерінде келесі шарттар орындалады: -шақырулар ағыны Пуассон таратылымына бағынады; -шақырудың қызмет көрсету ұзақтығы экспоненциалды таратылымға бағынады. Сонымен қоса әртүрлі модельдер бір-бірінен ерекшеленеді, егер желінің барлық арналары бос болмаса қабылданатын уақыт кезінде шақырулардың әртүрлі жағдайлары туады. Бұл шақырулар жойылуы мүмкін (керексіздік белгісімен желі моделі), немесе қатарға тұру және белгісіз ұзақ уақыт бойы арнаның босағанын күту, содан кейін керекті аралық уақыт көлемінде қызмет көрсету (күту белгісімен желі моделі); -аралық жағдайлар болуы мүмкін, мысалы, күту жағдайымен модельдер, бірақ шектеулі аралық уақыт көлемінде. Керексіздік белгісімен желі моделі (lost-calls-cleared-conditions -керексіздік алған шақыруларды өшіру шарты), ол – Эрланг В моделі деп те аталады. Бұл модельдегі бас тарту ықтималдығы (арналар бос емес кезіндегі шақырулардың түсу ықтималдығы) келесі формуламен анықталады:
Мұндағы N – арна саны, А = (λ)·(Т) - трафик. Арналардың барлығының бостығының ықтималдығы келесі формуламен анықталады:
К арналардың бос емес болу ықтималдығы келесі формуламен анықталады:
Бос емес арналардың орташа саны:
Күту жағдайымен желі моделі Эрланг С моделі деп аталады. Бұл модельдің кідіру уақыты (яғни, түсетін шақырудың бірден қызмет көрсетілмей кезекке тұру ықтималдығы) келесі формуламен анықталады:
мұндағы,
барлық арналардың бос болу ықтималдығы. Күту уақытын шектеуімен модель желісі, Эрланг А моделі немесе Пуассон моделі. Бұл модельде барлық арна бос емес жағдайында түскен шақыру кезекке тұрады, бірақ күту уақыты орташа қызмет көрсету уақытынан аспайды (сөйлесудің орташа ұзақтығы). Бұл уақыт ішінде кем дегенде бір арна босаса, шақыру орташа қызмет көрсету уақытының босаған бөлігіне орналасады, содан соң лақтырылады. Мұндай желідегі бас тарту ықтималдығы:
Ұялы мобильді байланыс желісіндегі сыйымдылықты есептегенде әдетте Эрланг В моделі қолданылады. Мұның себебі, Эрланг В және С модельдердің бас тартуының аз ықтималдығында бір-біріне жақын шешімдер беріледі, сонымен қоса бас тарту ықтималдығы Рв > 0,1 болғанда трафиктің салыстырмалы шамалы өсуі (А > 40) бас тарту ықтималдығының тез өсуіне әкеледі, яғни қызмет көрсету спасының тез төмендеуі. Сол үшін ұялы мобильді байланыс желісінде сыйымдылықты есептеу 0,01-ден 0,05-ке шейінгі Рв мәндері үшін анықталады. (5.6) - өрнектің үлкендігін ескере отырғанда, бас тарту желісіндегі шақырудың блоктау ықтималдығын анықтайтын түрі, әдетте тәжірибеде 6- кесте түрінде көрсетіледі:
6 – кесте. Эрланг В (бас тарту желісі – система с отказами)
|

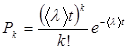 , (5.2)
, (5.2) , (5.3)
, (5.3) , (5.4)
, (5.4) , егер τ ≥ 0 (5.5)
, егер τ ≥ 0 (5.5)

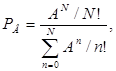 (5.6)
(5.6) , (5.7)
, (5.7) (5.8)
(5.8)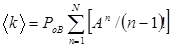 (5.9)
(5.9) (5.10)
(5.10) (5.11)
(5.11)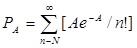 (5.12)
(5.12)


