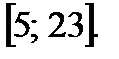Часть 2. Профильный уровень. В11.Найдите значение выражения при t = 25.
В11. Найдите значение выражения
В12. Максимальная скорость (в м/с) безопасного прохождения автомобилем дорожного поворота вычисляется по формуле В13. Найдите объём многогранника, вершинами которого являются точки D, E,F, D 1 , E 1 , F 1 правильной шестиугольной призмы ABCDEFA 1 B 1 C 1 D 1 E 1 F 1, площадь основания которой равна 8, а боковое ребро равно 9.
В14. К 200 г раствора, содержащего 60 % соли, добавили 300 г раствора, содержащего 50 % той же соли. Сколько процентов соли содержится в получившемся растворе? В15. Найдите наибольшее значение функции на отрезке [- 7,5; 0]. С1. а) Решите уравнение б) Найдите все корни этого уравнения, принадлежащие промежутку С2. В цилиндре высотой 5 и радиусом 6 проведено сечение, параллельное его оси и отсекающее от окружности основания дугу в 1200. Определите площадь этого сечения.
С3. Решите систему неравенств: С4. Диагональ АС прямоугольника АВСD с центром О образует со стороной АВ угол 300. Точка Е лежит вне прямоугольника, причём а) Докажите, что б) Прямая ОЕ пересекает сторону AD прямоугольника в точке К. Найдите ЕК, если известно, что ВЕ = 40 и СЕ = 24.
С5. Найдите все значения параметра а, при каждом из которых уравнение
С6. Бесконечная десятичная дробь устроена следующим образом. Перед десятичной запятой стоит нуль. После запятой подряд выписаны члены возрастающей последовательности натуральных чисел аn. В результате получилось рациональное число, которое выражается несократимой дробью, знаменатель которой меньше 100. Найдите наименьшее возможное значение а3.
|

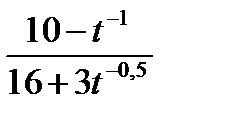 при t = 25.
при t = 25. где
где 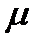 - коэффициент трения покоя между колесами автомобиля и дорогой, R – радиус поворота (м), g = 10 (м/с2) – ускорение свободного падения. При каком наименьшем коэффициенте трения движение со скоростью 54 км/ч на участке поворота дороги радиусом 90 м является безопасным?
- коэффициент трения покоя между колесами автомобиля и дорогой, R – радиус поворота (м), g = 10 (м/с2) – ускорение свободного падения. При каком наименьшем коэффициенте трения движение со скоростью 54 км/ч на участке поворота дороги радиусом 90 м является безопасным?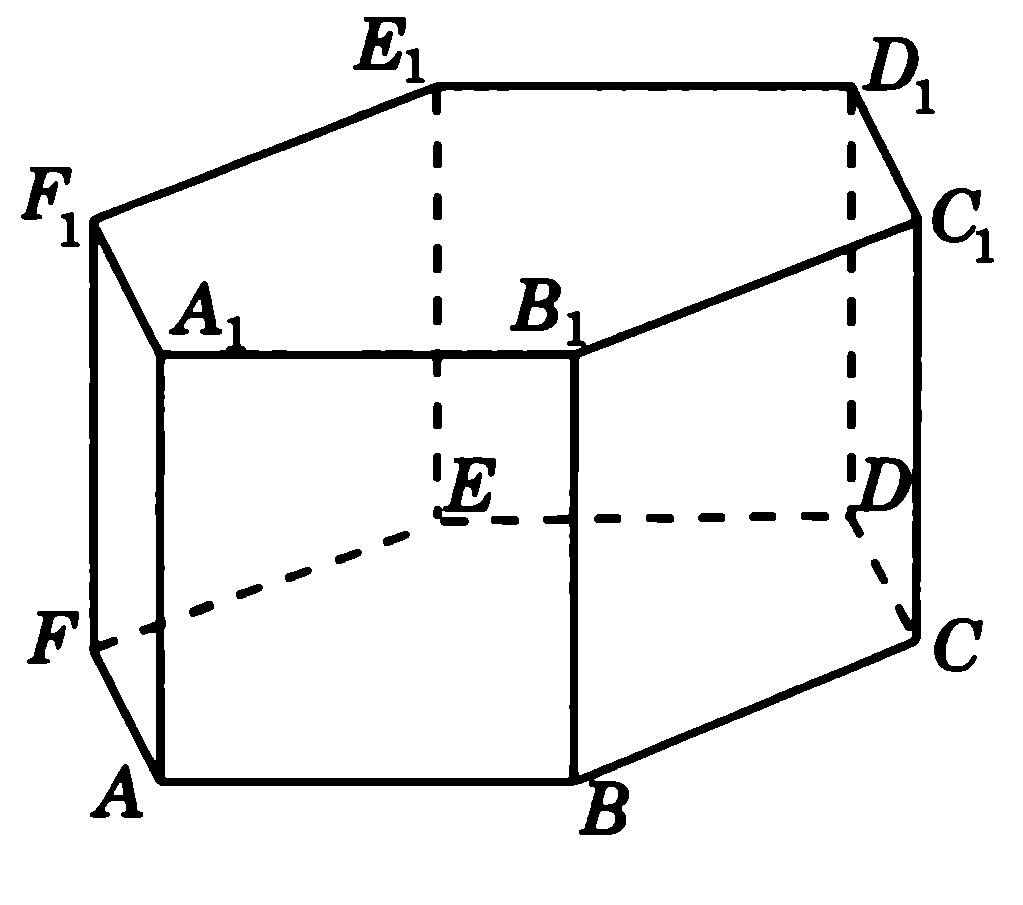

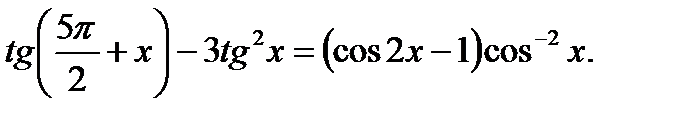
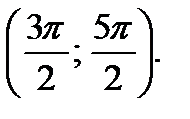
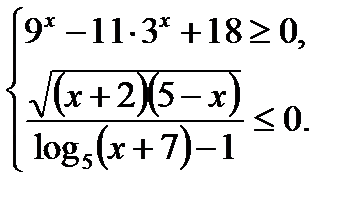
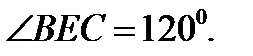

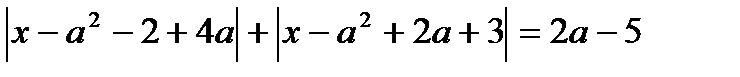 имеет хотя бы один корень на отрезке
имеет хотя бы один корень на отрезке