Основы алгебры логики и выполнения логических операций
Математическим аппаратом анализа и синтеза цифровых устройств служит алгебра логики, в которой любая переменная может иметь состояние "0" - логический ноль или "1" - логическая единица. В случае с одной переменной в алгебре логики действуют следующие правила, характеризующие операции: 1. Логическое сложение (дизъюнкция) Х + 0 = Х, Х + 1 = 1, Х + Х = Х, Х + 2. Логическое умножение (конъюнкция) Х · 0 = 0, Х · 1 = Х, Х · В случае двух или более переменных при анализе и преобразовании логических выражений используются следующие основные законы и тождества: 1. Переместительный закон. Х1 + Х2 = Х2 + Х1; Х1 · Х2 = Х2 · Х1. 2. Сочетательный закон. (Х1 + Х2) + Х3 = Х1 + (Х2 +Х3); (Х1 · Х2) · Х3 = Х1 · (Х2 · Х3). 3. Распределительный закон. Х3 (Х1 + Х2) = Х3 · Х1 + Х3 · Х2 ; Х1 + Х2 · Х3 = (Х1 + Х2) (Х1 + Х3). 4. Закон поглощения Х1 (Х1 + Х2) = Х1; Х1(Х1 + Х2) (Х1 + Х3) +... + (Х1 + Хn) = X1. 5. Закон склеивания (Х1 + Х2) (Х1 + Х1Х2 + Х1Х2 = Х1. 6. Закон де Моргана
Х1 + Х2=
Используя законы и тождества алгебры логики, можно сложное выражение привести к нормальной форме, содержащей сумму произведения или произведение сумм логических переменных. Логическое устройство, выходные функции которого однозначно определяются входными логическими функциями, в тот же момент времени называется комбинационным. Создание логических комбинационных устройств осуществляется по схеме: - по условию задачи составляется таблица истинности; - по таблице истинности составляется логическое уравнение; - производится минимизация функции; - составляется логическая схема. Пример. Дана функция y= (x1, x2) заданой таблично (табл.1.)
Логическая функция, заданная таблично или аналитически, может быть изображена на карте КАРНО, пердставляющей собой прямоугольник, разбитый на 2m клеток, где m - число аргументов функции. Если функция записана в СДНФ, то в клетки карты Карно, которые соответствуют минтермам, записываю единицы, а в остальные клетки записывают нули. При записи в СКНФ в клетки карты Карно, которые соответствуют макстермам, вписываются нули, в остальные клетки записывают единицы. На рис.2 показано такое отображение карт Карно.
Минимизация логических функций. Упрощение логических функций или их минимизация – это нахождение из всех возможных форм представления ЛФ такой формы, при которой обеспечивается минимум целевой функции (аппаратных затрат, быстродействия, экономичности и т.д.).На практике для этого используютя либо аналитический метод, либо карты Карно. Порядок выполнения работы: 1. Ознакомиться с лабораторным стендом УМ11. 2. Синтезировать минимизированную функционально-устойчивую комбинационную логическую схему, алгоритм функционирования которой задан следующей таблицей истинности (табл. 2)(по вариантам).
3. По таблице истинности составить уравнение y= (x1, x2 , x3) в совершенной дизъюктивной нормальной форме. 4. Провести минтмизацию ЛФ по карте Карно. 5. Построить минимизированную функцию в базе И-НЕ.
В отчете представить:
1. Материалы, относящиеся к минимизации ЛФ, структурная схема. 2. Составить схемы реализации элементов И, ИЛИ на базе элементов И-НЕ, и проверить правильность их функционирования. 3. Выводы.
|

 = 1
= 1 2) = Х1;
2) = Х1; =
=  ;
;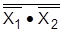 ; Х1 Х2=
; Х1 Х2= 

 Х1 *Х2
Х1 *Х2
 Х1 *Х2
Х1 *Х2
 Х1 + Х2
Х1 + Х2
 Х1 *Х2
Х1 *Х2




