Правило сложения дисперсий и его использование в анализе факторов.
Для оценки влияния факторов, определяющих вариацию, используют прием группировки: совокупность разбивают на группы, выбрав в качестве группировочного признака один из определяющих факторов. Тогда наряду с общей дисперсией, рассчитанной по всей совокупности, вычисляют внутигрупповую дисперсию (или среднюю из групповых) и межгрупповую дисперсию (или дисперсию групповых средних). 1) Общая дисперсия
2) Межгрупповая дисперсия измеряет систематическую вариацию, обусловленную влиянием фактора, по которому произведена группировка:
— — 3) Внутригрупповая дисперсия оценивает вариацию признака, сложившуюся по влиянием других, неучитываемых в данном исследовании факторов и независящую от фактора группировки. Она определяется как средняя из групповых дисперсий.
— Все три дисперсии (
на этом соотношении строятся показатели, оценивающие влияние признака группировки на образование общей вариации. К ним относятся эмпирический коэффициент детерминации ( Средняя внутригрупповых дисперсий характеризует случайную, не обусловленную признаком факторов вариацию.
В математической статистике доказывает правило сложения дисперсий, которое говорит, что общая дисперсия равна сумме межгрупповой дисперсии и средней внутригрупповых дисперсий:
Эмпирический коэффициент детерминации (
14. Понятие и виды динамических рядов, основные правила их построения. Основная цель статистического изучения динамики явлений состоит в выявлении и измерении закономерностей их развития во времени. Это достигается посредством построения и анализа статистических рядов динамики. Рядом динамики называются расположенные в хронологической последовательности статические показатели, отображающие развитие изучаемого явления во времени. Каждый ряд динамики содержит два основных элемента: 1)показатели времени t; 2)соответствующие им уровни развития изучаемого явления y. В качестве показаний времени в рядах динамики выступают а) либо определенные даты времени; б)либо определенные периоды; В соответствии с этим ряды динамики по виду делятся на: -моментные, интервальные. 1)Моментные ряды динамики отображают уровни динамического ряда на дату. Списочная численность работников предприятия в 2013г.
2) Интервальный ряд динамики содержит значения показателей за определенные периоды времени. В интервальном ряду уровни можно суммировать, получая объем явления за более длительный период, или так называемые накопленные итоги. Розничный товарооборот магазина в 2008-2013гг.
Статическое отображение развития явления во времени может быть также представлено рядами динамики с нарастающими итогами. Их применение обусловлено потребностями отображения результатов развития показателей не только за данный период, но и с учетом предшествующих периодов. При составлении таких рядов производится последовательное суммирование смежных уровней. Уровни рядов динамики могут выражаться абсолютными, относительными или средними величинами. По виду показателя уровня ряды динамики подразделяются на ряды динамики абсолютных, относительных и средних величин. Главными условиями построения рядом динамики является их сопоставимость. Поэтому при построении рядов динамики должны соблюдаться правила,обеспечивающие сопоставимость рядов. Основные правила следующие: 1. Обеспечение одинаковой полноты охвата различных частей явления. 2. Учет одинаковости границ территорий. 3. При определении сравниваемых уровней ряда динамики необходимо использовать единую методологию их расчета; 4. Использование одинаковых единиц измерения. 5. Равенство периодов,за которое приводится данные, является одним из условий сопоставимости уровней интервального динамического ряда.
|

 характеризует вариацию признака во всей совокупности, сложившуюся под влиянием всех факторов и условий.
характеризует вариацию признака во всей совокупности, сложившуюся под влиянием всех факторов и условий.
 групповые средние,
групповые средние, численность единиц i-й группы
численность единиц i-й группы
 дисперсия i-ой группы.
дисперсия i-ой группы.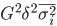 ) связаны между собой следующим равенством, которое известно как правило сложения дисперсий:
) связаны между собой следующим равенством, которое известно как правило сложения дисперсий:
 ) и эмпирическое корреляционное отношение (
) и эмпирическое корреляционное отношение ( ).
).





