Девятый теоретический опрос
Знать формулы:расстояние от точки до плоскости, расстояние между двумя параллельными плоскостями, угол между двумя плоскостями, угол между двумя прямыми, угол между прямой и плоскостью.
II. Образцы вариантов контрольных и самостоятельных работ Образец самостоятельной работы по теме «Векторная алгебра». 1) А … D 1 – параллелепипед. 2) АМ – медиана треугольника АВС 3) Найти расстояние от точки А (3,4, –1) до прямой (ВС), если В (2,0,3), С (–3,5,4). (система координат прямоугольная декартова) 4) АВСА 1 В 1 С 1 - призма, М и Р – середины АА 1 и А 1 С 1, Н – точка пересечения диагоналей грани ВСС 1 В 1. Найти отношение объемов данной призмы и тетраэдра ВМРН.
Образец самостоятельной работы по теме «Метод координат». 1) Дана прямоугольная декартова система координат. Определить вид четырехугольника АВСD, если А(1,-2), В(3,4) С(9,2), D(7,-4). 2) АВСD – квадрат, О – точка пересечения его диагоналей. Выяснить существуют ли точки, имеющие одинаковый координаты в двух системах координат
Образец контрольной работы по темам «Прямая на плоскости. Прямые и плоскости в пространстве» 1) АВСD – квадрат. Зная, что А (0,-3), АВ:4х – у – 3 = 0 и CD:4х – у – 5 = 0, составить уравнения прямых АD и ВС. 2) Луч света направлен по прямой а: х + у – 2 = 0. Дойдя до прямой b: 3х – 4у + 1= 0, он отражается и скользит по прямой р. Найти уравнение прямой р. 3) Найти точку, симметричную точке (3,5) относительно прямой 5х + 4у + 6 = 0. 4) Составить уравнение плоскости, проходящей через прямую х = 1 + 2t, y = -1 + 3t, z = 4t и параллельной оси OZ. 5) Составить уравнение прямой, проходящей через точку А(1, 1, 1) параллельной плоскости 2x + 3y –5z + 1 = 0 и пересекающей прямую x = 3 + 3t,y = –2 + t, z=4 – 2t. 6) Выяснить взаимное расположение прямой x = 1 + 2t, y = -5 + 4 t, z = t и плоскости х + 2у – 10z + 3 = 0.
|

 ,
,  ,
,  . О – точка пересечения диагоналей грани А 1 В 1 С 1 D 1, М – середина DС. Найти координаты вектора
. О – точка пересечения диагоналей грани А 1 В 1 С 1 D 1, М – середина DС. Найти координаты вектора 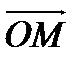 в базисе {
в базисе {  ,
,  ,
,  }
} (2,3, –1),
(2,3, –1),  (4, –1,3) Найти угол АМС. (базис ортонормированный).
(4, –1,3) Найти угол АМС. (базис ортонормированный). к системе координат
к системе координат 



