Обработка результатов. Задание
Внимательно рассмотрев изображение спектра, выделить канты, принадлежащие различным колебательным сериям (e,υ → e',υ' и e,υ+1 → e',υ') Заметим, что при использовании шкалы длин волн для разделения кантов по сериям мы фактически полагаем, что спектр эквидистантен в шкале длин волн, что, вообще говоря, неверно. Энергетический спектр осциллятора эквидистантен в энергетической шкале. Однако, поскольку длины волн соседних кантов данной серии близки, то в узком диапазоне длин волн можно считать, что спектр приблизительно эквидистантен и в шкале длин волн. Поэтому, последовательно переходя от одного узкого интервала к другому, мы можем визуально выделить колебательные серии. Методически правильно было бы поступить иначе: выделение колебательных серий произвести на основании анализа измеренных в эксперименте волновых чисел кантов. Однако этот путь требует высокой точности при определении их длин волн, которая не достигается в условиях нашего эксперимента и обработки его результатов. Поэтому выбран визуальный метод выделения колебательных серий. Длины волн кантов колебательных полос определяются по впечатанной шкале. Если кант находится в промежутке между двумя штрихами с отметками длин волн, то пользуются методом линейной интерполяции (рис.11).
Пример такого расчета для некоторой серии e,υ → e',υ' приведен в таблице. В спектроскопии принято пользоваться волновыми числами в см-1, т.к. числа при этом получаются меньшими, чем частоты и с ними удобнее работать. В тоже время энергия кванта оказывается пропорциональной волновому числу: Е = hν = h
Таблицу, аналогичную этой, составляют для серии полос e,υ+1 → e',υ'. Используя полученные экспериментальные результаты найти: 1. Энергетический интервал между двумя колебательными уровнями возбужденного электронного состояния. При этом нужно учесть, что ΔWυ'=hc 2. Построить график, подобный изображенному на рис.6. Для обеспечения необходимой точности масштабы выбирают 100 см-1 в 0.5 см по оси абсцисс и 2 см-1 в 0.5 см по оси ординат По наклону прямолинейного участка графика Здесь 3, Из графика по смещению кривых для разных серий e,υ → e',υ', e,υ+1 → e',υ' находят величину волнового числа, соответствующего колебательному кванту энергии W= h 4. По длинноволновой границе кантов с учетом поправок на нулевые уровни энергии в е и е' находят величину электронного перехода в молекуле йода 5. Зная коротковолновую границу схождения полос λгр и найдя энергию электронного перехода 6. Определить на снимке какое оттенение кантов: красное или фиолетовое, и соответственно сделать заключение о соотношении В'>В или В'<В. Сделать вывод об изменении межатомного расстояния при электронном возбуждении молекулы. 7. Определить при помощи микроскопа расстояние между вращательными уровнями в молекуле, и, учитывая материал п.2, оценить межатомное расстояние в молекуле йода. Если на графике провести экстраполяции величины кванта колебательной энергии Как легко видеть из формулы (20), график должен представлять собой прямую лишь при υ'x' «νυ. По мере увеличения номера влияние отброшенных в (20) членов становится существенным, и линия графика изгибается. 8. Следует отметить, что размеры молекул можно оценить не только по вращательным уровням, но и по уровням колебательной энергии. Согласно принципу неопределенности, частица, локализованная с точностью r, имеет импульс p ~ ћ/r, и тогда ее энергия Поскольку D' известно, можно определить 9. Таким образом, определив величину колебательного кванта энергии, постоянную ангармоничности, величину энергии диссоциации (т.е. глубину потенциальной ямы), получаем полное описание потенциала взаимодействия ядер в молекуле в данном электронном состоянии. Используя имеющуюся информацию о молекуле йода, построить кривую потенциала для возбужденного электронного состояния. Литература 1. Белый М.У., Охрименко Б.А. Атомная физика.- Киев:Вища школа, - I984. – Гл. 9. 2. Волькенштейн М.В. Строение и физические свойства молекул.- М.-Л.; Изд-во АН СССР. 1955. - 231 с. 3. Герцберг Г. Спектры и строение двухатомных молекул.- М.:Изд-во иностр. лит., 1948. - 297 с. 4. Кондратьев В.И. Структура атомов и молекул. -М: Физматгиз, 1959.- 524 с. Контрольные вопросы 1. Дайте определение энергии диссоциации молекулы. 2. Укажите известные Вам способы определения энергии диссоциации молекул. 3. Какие силы обеспечивают устойчивость молекул? 4. Почему колебания ядер молекулы не могут быть гармоническими? 5. Объясните происхождение энергетических уровней различного типа в молекулах. 6.Какова структура электронно-колебательного спектра поглощения молекулы? 7. Что Вы знаете о распределении молекул по колебательным уровням? 8. Изложите идею оптического метода определения энергии диссоциации. 9. Как экспериментально оценить энергию колебательного кванта молекулы? 10. Почему в данной работе использован прибор с высокой разрешающей способностью?
|

 Для этого измеряют на компараторе расстояние в делениях ∆ п = п2-п1 (п1 , п2 - отсчеты по компаратору) между двумя штрихами на шкале длин волн. Расстояние между двумя штрихами соответствует 2 нм. Разделив 2 нм на ∆n, получают цену одного деления компаратора в нм. Измерив затем расстояние ∆х канта от ближайшего штриха на шкале длин волн, определяют длину волны канта по формуле λканта=λшкалы ±∆ х
Для этого измеряют на компараторе расстояние в делениях ∆ п = п2-п1 (п1 , п2 - отсчеты по компаратору) между двумя штрихами на шкале длин волн. Расстояние между двумя штрихами соответствует 2 нм. Разделив 2 нм на ∆n, получают цену одного деления компаратора в нм. Измерив затем расстояние ∆х канта от ближайшего штриха на шкале длин волн, определяют длину волны канта по формуле λканта=λшкалы ±∆ х  . Знак поправки выбирается сообразно относительному положению канта и штриха шкалы. Измеренные длины волн кантов заносят в таблицу, переводят в волновые числа.
. Знак поправки выбирается сообразно относительному положению канта и штриха шкалы. Измеренные длины волн кантов заносят в таблицу, переводят в волновые числа. c
c
 , где
, где  .
. находят постоянную ангармоничности хk осциллятора, соответствующего возбужденному электронному состоянию.
находят постоянную ангармоничности хk осциллятора, соответствующего возбужденному электронному состоянию. есть величина, представляющая собой разность волновых чисел
есть величина, представляющая собой разность волновых чисел  - соответствующая им разность колебательных квантовых чисел υ' в возбужденном электронном состоянии (она равна числу интервалов между экспериментальными точками на прямолинейном участке графика).
- соответствующая им разность колебательных квантовых чисел υ' в возбужденном электронном состоянии (она равна числу интервалов между экспериментальными точками на прямолинейном участке графика). на самый нижний уровень верхнего электронного состояния е'. Находят также коротковолновую границу λгр, соответствующую слиянию кантов и переходу к сплошному спектру.
на самый нижний уровень верхнего электронного состояния е'. Находят также коротковолновую границу λгр, соответствующую слиянию кантов и переходу к сплошному спектру. , можно определить энергиюдиссоциации молекулы в верхнем электронном состоянии е', т.е. величину D'. Необходимо снова учесть величину поправки на нулевой уровень энергии.
, можно определить энергиюдиссоциации молекулы в верхнем электронном состоянии е', т.е. величину D'. Необходимо снова учесть величину поправки на нулевой уровень энергии. к нулю, то получим значение волнового числа, соответствующего фотодиссоциации молекул йода. Экстраполяцию следует проводить двумя способами: "по точкам", а также продолжая линейную часть кривой. Разница между определенными такими способами значениями энергии диссоциации отражает точность теории, отбрасывающей поправки более высокого порядка, чем xk.
к нулю, то получим значение волнового числа, соответствующего фотодиссоциации молекул йода. Экстраполяцию следует проводить двумя способами: "по точкам", а также продолжая линейную часть кривой. Разница между определенными такими способами значениями энергии диссоциации отражает точность теории, отбрасывающей поправки более высокого порядка, чем xk.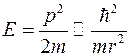 . Если амплитуда колебаний достигает величины порядка самой молекулы r0, то молекула диссоциирует. При этом энергия колебательного движения kr2 (k -константа упругой связи) становится порядка энергии связи молекулы E≈D', т.е. D'≈ћ2/mr2, откуда
. Если амплитуда колебаний достигает величины порядка самой молекулы r0, то молекула диссоциирует. При этом энергия колебательного движения kr2 (k -константа упругой связи) становится порядка энергии связи молекулы E≈D', т.е. D'≈ћ2/mr2, откуда  .
. - размер молекулы в возбужденном электронном состоянии. Вычислить эту величину и сравнить ее с полученным ранее значением.
- размер молекулы в возбужденном электронном состоянии. Вычислить эту величину и сравнить ее с полученным ранее значением.


