Состояние атома в целом характеризуется суммарным значением орбитального  и спинового
и спинового  моментов электронов. Двухатомная молекула имеет осевую симметрию. Поэтому в случае двухатомной молекулы говорят о проекции суммарного орбитального момента
моментов электронов. Двухатомная молекула имеет осевую симметрию. Поэтому в случае двухатомной молекулы говорят о проекции суммарного орбитального момента  на ось молекулы, обозначая эту проекцию через
на ось молекулы, обозначая эту проекцию через  . Электронные состояния молекулы классифицируют по значению квантового числа
. Электронные состояния молекулы классифицируют по значению квантового числа  . В случае атома состояния с квантовыми числами L = 0, 1, 2, 3,... обозначают буквами S,P,D,F,... Состояния молекулы с квантовыми числами
. В случае атома состояния с квантовыми числами L = 0, 1, 2, 3,... обозначают буквами S,P,D,F,... Состояния молекулы с квантовыми числами  =0, 1, 2, 3,… обозначают греческими буквами Σ, П, Δ, Ф….
=0, 1, 2, 3,… обозначают греческими буквами Σ, П, Δ, Ф….
При переходе молекулы из одного электронного состояния в другое одновременно происходит изменение колебательного и вращательного состояний.
Полагая, что в первом приближении имеет место аддитивность трех видов энергии, частоты отдельных линий электронного спектра можно описать формулой
 (16)
(16)
Здесь и дальше штрих (/) относится к обозначению верхнего возбужденного электронного состояния. Для двухатомной молекулы из (6) и (12) можно записать
 (17)
(17)
 (18)
(18)
Здесь следует обратить внимание на то, что константы верхнего электронного состояния отличаются от констант нижнего, т.е.  и
и 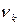 ,
,  и
и  ,
,  и В в общем случае немного отличаются друг от друга. Основное отличие состояний определяется изменением равновесного расстояния rо между ядрами при переходе молекулы из одного электронного состояния в другое. При электронном возбуждении молекулы rо обычно увеличивается.
и В в общем случае немного отличаются друг от друга. Основное отличие состояний определяется изменением равновесного расстояния rо между ядрами при переходе молекулы из одного электронного состояния в другое. При электронном возбуждении молекулы rо обычно увеличивается.
Без учета вращательной энергии для линии каждой полосы спектра можно записать (учитывал (16), (17))
 (19)
(19)
Если рассмотреть переходы с определенного колебательного уровня υ, характеризующего нижнее электронное состояние, на все возможные колебательные уровни верхнего состояния, то для
этой серии полос можно записать частоты переходов следующим образом
 (20)
(20)

 Характерной постоянной каждой системы полос является ν00 которая обусловлена переходом υ=0 ↔ υ / =0 и называется нулевой полосой. Как видно из формулы (19), отличие значений частоты нулевой линии, нулевой полосы и частоты сугубо электронного перехода νе обусловлено нулевой колебательной энергией молекулы (рис. 4). Следует отметить, что для незапрещенного электронного перехода возможны произвольные значения ∆υ, т.е. правило отбора для колебательного квантового числа υ не имеет места.
Характерной постоянной каждой системы полос является ν00 которая обусловлена переходом υ=0 ↔ υ / =0 и называется нулевой полосой. Как видно из формулы (19), отличие значений частоты нулевой линии, нулевой полосы и частоты сугубо электронного перехода νе обусловлено нулевой колебательной энергией молекулы (рис. 4). Следует отметить, что для незапрещенного электронного перехода возможны произвольные значения ∆υ, т.е. правило отбора для колебательного квантового числа υ не имеет места.

 и спинового
и спинового  моментов электронов. Двухатомная молекула имеет осевую симметрию. Поэтому в случае двухатомной молекулы говорят о проекции суммарного орбитального момента
моментов электронов. Двухатомная молекула имеет осевую симметрию. Поэтому в случае двухатомной молекулы говорят о проекции суммарного орбитального момента  . Электронные состояния молекулы классифицируют по значению квантового числа
. Электронные состояния молекулы классифицируют по значению квантового числа  (16)
(16) (17)
(17) (18)
(18) и
и 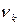 ,
,  и
и  ,
,  и В в общем случае немного отличаются друг от друга. Основное отличие состояний определяется изменением равновесного расстояния rо между ядрами при переходе молекулы из одного электронного состояния в другое. При электронном возбуждении молекулы rо обычно увеличивается.
и В в общем случае немного отличаются друг от друга. Основное отличие состояний определяется изменением равновесного расстояния rо между ядрами при переходе молекулы из одного электронного состояния в другое. При электронном возбуждении молекулы rо обычно увеличивается. (19)
(19) (20)
(20)
 Характерной постоянной каждой системы полос является ν00 которая обусловлена переходом υ=0 ↔ υ / =0 и называется нулевой полосой. Как видно из формулы (19), отличие значений частоты нулевой линии, нулевой полосы и частоты сугубо электронного перехода νе обусловлено нулевой колебательной энергией молекулы (рис. 4). Следует отметить, что для незапрещенного электронного перехода возможны произвольные значения ∆υ, т.е. правило отбора для колебательного квантового числа υ не имеет места.
Характерной постоянной каждой системы полос является ν00 которая обусловлена переходом υ=0 ↔ υ / =0 и называется нулевой полосой. Как видно из формулы (19), отличие значений частоты нулевой линии, нулевой полосы и частоты сугубо электронного перехода νе обусловлено нулевой колебательной энергией молекулы (рис. 4). Следует отметить, что для незапрещенного электронного перехода возможны произвольные значения ∆υ, т.е. правило отбора для колебательного квантового числа υ не имеет места.


