Вращательные спектры
Движение такой молекулы рассматривается как движение жесткого ротатора со свободной осью (рис. 2). Кинетическая энергия вращения двухатомной молекулы
где r1, r2 - расстояния от атомов до центра масс, r1+r2 = r0. Момент инерции молекулы
где μ- приведенная масса. Тогда кинетическая энергия
поскольку полная анергия молекулы определяется в этом случае ее кинетической энергией. Здесь М - момент количества движения. В соответствии сквантовой механикой, момент импульса квантуется следующим образом
где J - вращательное квантовое число. J =0, 1, 2 ,…. Изменения вращательного квантового числа должны удовлетворять правилам отбора ∆J =1. Одновременно квантуется и проекция момента импульса на выделенное направление z:
где магнитное квантовое число mJ =0, 1, 2,… и принимает 2J +1 значение. Подставляя (10) в (9), получаем
где Энергетические уровни вращающейся молекулы, в соответствии с (12), расположены не на одинаковых расстояниях: при увеличении вращательного квантового числа расстояние между уровнями растет. Частоты, которые излучаются или поглощаются молекулой при вращении, определяются формулой
где
где J = 0, 1, 2,… Таким образом, в случае модели жесткого ротатора вращательный спектр молекулы состоит из серии равноотстоящих линий. Первая из них расположена при 2В (J =0), а расстояние между последующими линиями также равно 2В. Соответствующие переходы представлены на рис. 3а, а спектр на рис. 3б.
Все вышесказанное справедливо для модели жесткого ротатора. Однако в действительности, вследствие действия центробежной силы происходит некоторое растяжение молекулы: оказывается, что разновесное состояние зависит от значения J. Этот факт приходится учитывать дополнительным слагаемым в формуле (12) для энергии вращения.
|

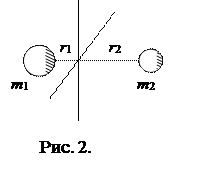 Кроме колебательных степеней свободы молекула обладает еще и вращательными. В первом приближении молекулу можно считать жесткой конструкцией из двух шариков массой т1 и m2 (если это атомы разного сорта), находящимися на фиксированном расстоянии r0 друг от друга. Молекула в этом случае способна вращаться относительно осей, которые проходят через ее центр масс.
Кроме колебательных степеней свободы молекула обладает еще и вращательными. В первом приближении молекулу можно считать жесткой конструкцией из двух шариков массой т1 и m2 (если это атомы разного сорта), находящимися на фиксированном расстоянии r0 друг от друга. Молекула в этом случае способна вращаться относительно осей, которые проходят через ее центр масс.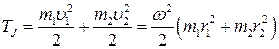 (7)
(7) , (8)
, (8) (9)
(9) (10)
(10) (11)
(11) (12)
(12) (13)
(13)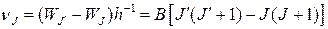 (14)
(14) - вращательные энергии верхнего инижнего состояний. Учитывая правила отбора и полагая, что J'>J для частоты вращательного движения получим
- вращательные энергии верхнего инижнего состояний. Учитывая правила отбора и полагая, что J'>J для частоты вращательного движения получим (15)
(15) Измерив расстояние между двумя линиями вращательного спектра, найдем, что это число должно быть равным 2В. А следовательно, из (13) можно найти момент инерции молекулы I. Если воспользоваться значением приведенной массы (см. формулу (6)), можно найти расстояние между атомами в молекуле.
Измерив расстояние между двумя линиями вращательного спектра, найдем, что это число должно быть равным 2В. А следовательно, из (13) можно найти момент инерции молекулы I. Если воспользоваться значением приведенной массы (см. формулу (6)), можно найти расстояние между атомами в молекуле.


