Символьные конструкции
Алфавитом будем называть любое конечное множество попарно различных знаков, называемых буквами (символами) этого алфавита. Алфавит будем обозначать заглавными буквами, например:
Символом l будем обозначать пустой символ. Словом в данном алфавите называется любая конечная (в том числе и пустая) последовательность букв этого алфавита. Слова будем обозначать малыми греческими буквами. Например: a = алгоритм – слово в алфавите А; b = 1010100 – слово в алфавите В; Пустое слово будем обозначать L. Длина слова a (обозначается |a|) – это количество букв в слове. Определим некоторые отношения и операции над словами. Равенство слов в алфавите А определяется индуктивно: а) пустые слова равны б) если слово a равно слову b, то a b =b b, где b –буква в алфавите А. Если слово a является частью слова b, то говорят, что имеет место вхождение слова a в слово b (слово a называется подсловом слова b). Это можно записать следующим образом: Слово a называется началом слова b, если Операция (и результат) приписывания слов a и b друг к другу называется конкатенацией (обозначается a||b). Например, если Определение машины Тьюринга (МТ) Под машиной Тьюринга понимается некоторая гипотетическая (абстрактная) машина, состоящая из следующих частей: 1) бесконечной в обе стороны ленты, разбитой на ячейки, в каждой из ячеек может быть записан только один символ из алфавита 2) рабочей головки или управляющего устройства (УУ), которое в каждый момент времени может находиться в одном из состояний множества
Машина Тьюринга
Функционирование МТ состоит из последовательности элементарных шагов (тактов). На каждом шаге выполняются следующие действия: 1) управляющее устройство считывает (обозревает) символ 2) в зависимости от своего состояния УУ вырабатывает символ 3) головка перемещается на одну ячейку вправо (R), влево (L) или остается на месте (E); 4) головка переходит в другое внутреннее состояние Состояние Полное состояние МТ называется конфигурацией. Это распределение букв по ячейкам ленты, состояние рабочей головки и обозреваемая ячейка. Конфигурация в такте t записывается в виде: Для описания работы МТ существует 3 способа: 1) система команд вида 2) функциональная таблица; 3) граф (диаграмма) переходов. С помощью МТ можно описывать выполнение арифметических операций над числами. При этом числа представляются на ленте, как слова в алфавите, состоящем из цифр какой-нибудь системы счисления, и разделяющихся специальным знаком, не входящем данный алфавит, например, Наиболее употребительной является унарная система, состоящая из одного символа – Пример 1. Операция сложения двух чисел в унарном коде. Начальная конфигурация: Система команд при
Комментарий к системе команд 1. Если в обозреваемой ячейке записан символ 2. Если в обозреваемой ячейке записан символ 3. Если в обозреваемой ячейке записан символ, записан символ 4. Если в обозреваемой ячейке записан символ 5. Если в обозреваемой ячейке записан символ 6. Если в обозреваемой ячейке записан символ
Описание МТ в виде функциональной таблицы:
Описание МТ в виде диаграммы переходов
Вычисление на МТ словарной функции Числовая функция
|


 – слово в алфавите С.
– слово в алфавите С. , где
, где 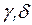 – слова в алфавите А.
– слова в алфавите А. ; концом слова b, если
; концом слова b, если  . Слово длины n, составленное из буквы а, повторенной n раз, будем обозначать
. Слово длины n, составленное из буквы а, повторенной n раз, будем обозначать  , например xyxxxyyyy =
, например xyxxxyyyy =  .
. .
. , а также пустой символ l;
, а также пустой символ l; . В каждом из состояний головка размещается напротив ячейки и может считывать (обозревать) или записывать в нее букву из алфавита А.
. В каждом из состояний головка размещается напротив ячейки и может считывать (обозревать) или записывать в нее букву из алфавита А.
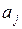 ;
; и обозреваемого символа
и обозреваемого символа  и записывает его в обозреваемую ячейку (возможно
и записывает его в обозреваемую ячейку (возможно  );
); (возможно
(возможно  ).
). называется начальным,
называется начальным,  – заключительным. При переходе в заключительное состояние машина останавливается.
– заключительным. При переходе в заключительное состояние машина останавливается. , где
, где  – подслово слева от обозреваемой ячейки,
– подслово слева от обозреваемой ячейки,  – подслово справа. Начальная конфигурация
– подслово справа. Начальная конфигурация  и конечная
и конечная  называются стандартными.
называются стандартными.
 .
. . Число Х в унарной системе счисления на ленте записывается словом
. Число Х в унарной системе счисления на ленте записывается словом  , (сокращенно
, (сокращенно  ) в алфавите А={
) в алфавите А={  }.
}. . Конечная конфигурация:
. Конечная конфигурация:  , т.е. сложение фактически сводится к приписыванию числа b к числу a. Для этого первый символ
, т.е. сложение фактически сводится к приписыванию числа b к числу a. Для этого первый символ  и
и 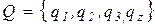 .
.
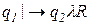 – стирание первого символа
– стирание первого символа 
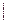 и МТ находится в состоянии
и МТ находится в состоянии  , тогда состояние изменяется на
, тогда состояние изменяется на  , обозреваемый символ заменяется на пустой, УУ сдвигается вправо.
, обозреваемый символ заменяется на пустой, УУ сдвигается вправо. – стирание символа
– стирание символа  , первый аргумент равняется 0.
, первый аргумент равняется 0. , обозреваемый символ заменяется на пустой, УУ сдвигается вправо.
, обозреваемый символ заменяется на пустой, УУ сдвигается вправо. – сдвиг вправо.
– сдвиг вправо. – стирание символа
– стирание символа  , и обозреваемый символ заменяется на
, и обозреваемый символ заменяется на  – сдвиг влево.
– сдвиг влево. , тогда состояние и обозреваемый символ не изменяются, УУ сдвигается влево.
, тогда состояние и обозреваемый символ не изменяются, УУ сдвигается влево. –
– и МТ находится в состоянии
и МТ находится в состоянии 








 будем понимать следующим образом. Пусть в начальной конфигурации на ленте записано слово
будем понимать следующим образом. Пусть в начальной конфигурации на ленте записано слово  . Если значение
. Если значение  определено, то конечного числа шагов (тактов) машина должна перейти в заключительную конфигурацию, в которой на ленте записано слово
определено, то конечного числа шагов (тактов) машина должна перейти в заключительную конфигурацию, в которой на ленте записано слово 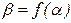 . В противном случае МТ должна работать бесконечно.
. В противном случае МТ должна работать бесконечно.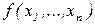 правильно вычислима (или просто вычислима) по Тьюрингу, если существует МТ, которая переводит конфигурацию
правильно вычислима (или просто вычислима) по Тьюрингу, если существует МТ, которая переводит конфигурацию 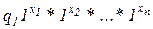 в конфигурацию
в конфигурацию  , когда
, когда  не определена.
не определена.


