Разветвление или условный переход в композиции машин Тьюринга
Если заданы машины Тьюринга
Разветвление машин Тьюринга на схемах композиции изображается следующим образом:
и обозначается
4. Цикл в композиции машин Тьюринга Цикл в композиции МТ реализуется по тем же принципам, что и разветвление. Циклическим будем считать следующий алгоритм «пока P(a)= ” true”, выполнять где a – слово на ленте перед первым выполнением Для изображения цикла введем некоторые обозначения, пусть:
Тогда, циклическая композиция машин Тьюринга или цикл, может быть изображена следующим образом:
Программирование с помощью композиций машин Тьюринга: 1) построение блок-схем сложных алгоритмов такой степени детализации, что их блоки соответствуют элементарным МТ; 2) построение элементарных МТ, реализующих простые блоки; 3) объединение элементарных МТ в композицию МТ. Пример. Записать композицию МТ для реализации функции z=y*x.
Следует отметить, что в любом случае необходимо в начале выполнения алгоритма выполнить проверку входных данных на корректность (например, равенство 0 аргумента при делении).
|

 и
и  , вычисляющие словарные функции
, вычисляющие словарные функции  и
и  , и машина
, и машина  , вычисляющая некоторый предикат P(a) с восстановлением (т.е. без стирания слова a), то для реализации разветвления может быть построена машина Тьюринга
, вычисляющая некоторый предикат P(a) с восстановлением (т.е. без стирания слова a), то для реализации разветвления может быть построена машина Тьюринга  , вычисляющая функцию:
, вычисляющая функцию:

 , здесь
, здесь  – результат работы машины
– результат работы машины  – машина Тьюринга, реализуюшая копирование входного слова
– машина Тьюринга, реализуюшая копирование входного слова  .
. »,
», – машина Тьюринга, реализующая вычисление предиката P(a);
– машина Тьюринга, реализующая вычисление предиката P(a); ;
;


 – МТ, реализующая функцию установки константы ноль;
– МТ, реализующая функцию установки константы ноль;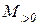 – МТ, вычисляющая предикат с восстановлением
– МТ, вычисляющая предикат с восстановлением  ;
;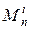 – МТ, реализующая функцию выбора
– МТ, реализующая функцию выбора  -того аргумента из
-того аргумента из  аргументов;
аргументов; – МТ, реализующая функцию уменьшение аргумента
– МТ, реализующая функцию уменьшение аргумента  на 1 в унарном коде (вытирает крайний левый символ
на 1 в унарном коде (вытирает крайний левый символ  );
); – МТ, выполняющая сложение двух чисел в унарном коде.
– МТ, выполняющая сложение двух чисел в унарном коде.


