Примитивно-рекурсивные функции
В качестве простейших функций в теории рекурсивных функций приняты следующие: 1. 2. 3. Оператор суперпозиции (подстановки) Суперпозицией функций
Оператор примитивной рекурсии
Примитивно-рекурсивная функция – арифметическая функция, которая может быть получена из простейших с помощью конечного числа применений операторов суперпозиции и примитивной рекурсии. Примитивно-рекурсивные функции являются всюду определенными. Пример 1. Константа a получается путем суперпозиции функций
Пример 2. Операция сложения
Таким образом, функция Пример 3. Примитивная рекурсивность операции умножения
Пример 4. Примитивная рекурсивность операции возведения в степень
Пример 5. Операция вычитания не является примитивно-рекурсивной, т.к. она не всюду определена: результат операции a-b при Арифметическое вычитание:
Для доказательства примитивной рекурсивности
т.е. операция Дополнительное свойство:
арифметическое вычитание – примитивно-рекурсивно. Пример 6. Функция
Функция
Пример 7. Примитивная рекурсивность функций
Отношение
Пример 8. Отношение Действительно, Отношение Действительно, Отношение Действительно, Оператор минимизации (m-оператор, оператор наименьшего корня) определяет новую арифметическую функцию Зафиксируем набор значений аргументов
Наименьшее целое неотрицательное значение
Говорят, что функция
Оператор минимизации работает бесконечно в одном из следующих случаев: 1) значение 2) значение 3) значение Оператор минимизации является удобным средством получения обратных функций: вычитание, деление, извлечение корня и так далее. Пример 9. Определение операции «вычитание»:
Пример 10. Определение операции «деление»:
Пример 11. Определение операции «извлечение корня»:
Пример 21. Определение операции «логарифм»:
Пример 13. Процесс вычисления функции с помощью оператора минимизации приведен ниже:
Частично-рекурсивная функция – функция, которая может быть построена из простейших с помощью конечного числа применений оператора суперпозиции, примитивной рекурсии и минимизации. Частично-рекурсивная функция является не всюду определенной, причем там, где она не определена, процесс ее вычисления продолжается бесконечно. Общерекурсивная функция –всюду определенная частично-рекурсивная функция. Связь между алгоритмами и рекурсивными функциями выражается тезисом Черча: какова бы ни была вычислимая неотрицательная целочисленная функция от неотрицательных целочисленных аргументов, существует тождественно равная ей частично-рекурсивная функция.
|

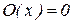 – константа «ноль».
– константа «ноль».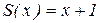 – «последователь».
– «последователь». – функция тождества или выбора аргумента, проекция.
– функция тождества или выбора аргумента, проекция. – подстановка в функцию от
– подстановка в функцию от  переменных
переменных  переменных, что дает новую функцию от
переменных, что дает новую функцию от  и
и  называют функцию:
называют функцию: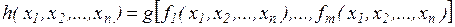 ;
;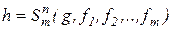 .
. , определяющий значение функции
, определяющий значение функции  , записывается в виде следующей схемы:
, записывается в виде следующей схемы:
 и
и  :
:
 может быть определена с помощью оператора примитивной рекурсии:
может быть определена с помощью оператора примитивной рекурсии:
 получена из простейших
получена из простейших  и
и  доказывается с использованием сложения:
доказывается с использованием сложения:
 доказывается следующим образом:
доказывается следующим образом:
 не определен в области натуральных чисел. Однако примитивно-рекурсивной является так называемое арифметическое (усеченное) вычитание или разность.
не определен в области натуральных чисел. Однако примитивно-рекурсивной является так называемое арифметическое (усеченное) вычитание или разность.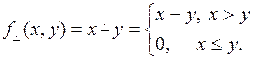
 вначале рассмотрим операцию
вначале рассмотрим операцию  :
:  ;
;

 – примитивно-рекурсивна.
– примитивно-рекурсивна. .
.
 – аналог функции
– аналог функции  для натуральных чисел.
для натуральных чисел.
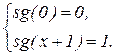
 – антисигнум, функция обратная
– антисигнум, функция обратная 
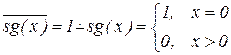 .
. ,
,  и модуль разности двух чисел доказывается с помощью арифметического вычитания:
и модуль разности двух чисел доказывается с помощью арифметического вычитания:
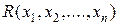 называется примитивно-рекурсивным, если примитивно-рекурсивна его характеристическая функция
называется примитивно-рекурсивным, если примитивно-рекурсивна его характеристическая функция 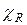 :
:
 – примитивно-рекурсивно.
– примитивно-рекурсивно.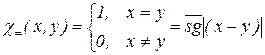 .
.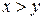 примитивно-рекурсивно.
примитивно-рекурсивно.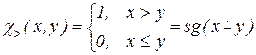 .
. примитивно-рекурсивно.
примитивно-рекурсивно. .
. от n переменных с помощью ранее построенной арифметической функции
от n переменных с помощью ранее построенной арифметической функции  от n+1 переменных. Пусть существует некоторый механизм вычисления функции
от n+1 переменных. Пусть существует некоторый механизм вычисления функции 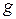 , причем значение функции
, причем значение функции  и рассмотрим уравнение относительно y:
и рассмотрим уравнение относительно y:  ; чтобы найти решение этого уравнения, натуральное
; чтобы найти решение этого уравнения, натуральное 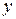 , будем вычислять последовательность значений:
, будем вычислять последовательность значений: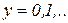 ..
.. , удовлетворяющее этому уравнению:
, удовлетворяющее этому уравнению:  обозначим:
обозначим: .
. .
. не определено;
не определено; для
для  определены, но не равны нулю, а значение
определены, но не равны нулю, а значение  – не определено;
– не определено; , но не равны нулю.
, но не равны нулю. .
.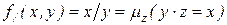 .
. .
.





