Задание на лабораторную работу
1. Разработать алгоритм вычисления 2. Проверить модель алгоритма на множестве тестовых примеров. 3. Определить к какому классу рекурсивных функций принадлежит
Варианты заданий 1. Сумма всех четных делителей числа 2. Количество всех нечетных делителей числа 3. Количество нулей в двоичной записи 4. Сумма цифр в двоичной записи 5. Количество взаимно-простых с 6. Максимальная цифра в 8-ричной записи числа 7. Минимальная цифра в 8-ричной записи числа 8. Количество четных цифр в 8-ричной записи числа 9. Количество нечетных цифр в 8-ричной записи числа 10. Сумма простых делителей числа 11. Количество простых делителей числа 12. Количество простых чисел, 13. Количество чисел, являющихся полными квадратами, 14. Сумма чисел, являющихся степенью двойки, 15. Максимальная цифра в 16-ричной записи числа 16. Минимальная цифра в 16-ричной записи числа 17. Ближайшее к 18. Произведение делителей числа 19. Произведение простых делителей числа 20. Произведение взаимно-простых с 21. Наименьшее общее кратное двух чисел, 22. Наибольший общий делитель двух чисел, 23. Функция, отличная от нуля в конечном числе точек. 24. Номер наибольшего простого делителя числа 25. Функция, вычисляющая целую часть квадратного корня от аргумента,
Контрольные вопросы 1. Что такое вычислимая, арифметическая, частичная или всюду определенная функция? 2. Определить операторы суперпозиции и примитивной рекурсии. 3. Перечислить простейшие функции теории рекурсивных функций. 4. Что такое примитивно-рекурсивные функции? 5. Показать примитивную рекурсивность известных арифметических функций. 6. Показать примитивную рекурсивность арифметизованных логических функции. Примитивная рекурсивность отношений и предикатов. 7. Определить оператор минимизации, в каких случаях он работает бесконечно? 8. Что такое частично-рекурсивная функция и общерекурсивная? 9. Сформулировать тезис Черча. 10. Определите соотношение между примитивно, частично и общерекурсивными функциями. Лабораторная работа № 2
|

 в виде рекурсивной функции.
в виде рекурсивной функции. .
.
 ,
, 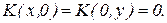


 .
.


