МЕТОДИЧЕСКИЕ УКАЗАНИЯ ДЛЯ ВЫПОЛНЕНИЯ КОНТРОЛЬНОЙ РАБОТЫ

1. Классический способ подсчета вероятностей

 

Определение: Событие называется случайным по отношению к данному испытанию, если при осуществлении этого испытания оно может произойти или не произойти.

Классическое определение вероятности. Если испытание сводится к полной группе равновозможных несовместных событий (классическая схема), то вероятность события А в данном испытании равна отношению числа элементарных исходов благоприятствующих появлению этого события к общему числу элементарных исходов испытания.

Вероятность события обозначают через Р (А). По определению

0≤Р(А)≤1 (1)

В формуле (1) m – число всех исходов благоприятствующих появлению событий А, n – общее число исходов испытания.

Задача 1. Брошен наудачу шестигранный игральный кубик. Найти: 1) вероятность появления цифры три на верхней грани игральной кости, 2) вероятность появления четного числа очков.

Решение: Испытание состоит в бросании игрального кубика. Всего шесть элементарных исходов испытания: выпадение цифры 1, 2, 3, 4, 5, 6. Эти исходы являются: несовместными, так как никакие два не произойдут одновременно; равновозможными, так как бросают кубик наудачу (никакой из исходов не имеет предпочтений в появлении перед остальными); перечисленные шесть исходов образуют полную группу событий, так как в результате испытания произойдет хотя бы один из них. Таким образом, имеет место классическая схема.

1. Пусть событие А – появление цифры три на верхней грани кубика. Вероятность этого события можно вычислить по формуле (1), где m = 1, а п=6. Следовательно, Р (А) = .

2. Событие В – появление четного числа очков на верхней грани кубика. Вероятность этого события вычислим по той же формуле (1), где m = 3, так как событию благоприятствуют исходы: появление цифры 2, цифры 4, цифры 6, а n=6. Следовательно Р(В)= = .

Задача 2. В группе 25 студентов. Из них по контрольной работе 20 студентов получили хорошие и удовлетворительные оценки, остальные не справились с предложенной работой. Какова вероятность того, что два студента, вызванных к доске, имеют неудовлетворительные оценки по контрольной работе.

Решение: Имеет место классическая схема. Испытание состоит в выборе двух студентов из 25 человек. Общее число возможных элементарных исходов испытания равно числу способов выбора из 25 человек двух студентов. В комбинациях из 25 человек по два важен состав, но безразличен порядок. Такие комбинации в комбинаторике называются сочетаниями и их число можно подсчитать по формуле числа сочетаний из n элементов по m:

(2)

Где n=25, m = 2 и, следовательно, С²₂₅= = = =300.

Пусть событие А – два вызванных к доске студента имеют неудовлетворительные оценки. Вероятность этого события подсчитаем по формуле (1). Общее число элементарных исходов испытания подсчитано выше, а число элементарных исходов благоприятствующих появлению события А – число способов выбрать двух студентов имеющих неудовлетворительные оценки из общего числа студентов несправившихся с контрольной работой. Число таких комбинаций подсчитаем по формуле (2), где n=25-20=5, а m=2.

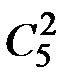= = = =10. Итак, Р(А)= = .