контрольной работы №1
Даны матрицы
А=
Найти значение α, при котором определитель матрицы А’В+ αЕ равен нулю (А’ − транспонированная матрица для матрицы А, Е − единичная матрица 4-го порядка). Решение. Сначала транспонируем матрицу А. Матрица А’ есть матрица, полученная из данной заменой каждой ее строки столбцом с тем же номером: А'= Далее перемножаем матрицу А’ на матрицу В. Заметим, что операция умножения двух матриц вводится только для случая, когда число столбцов первой матрицы равно числу строк второй матрицы. Произведением матрицы U=(uij) размером m×n на матрицу V=(vjk) размером n×p называется матрица W=(wik) размером m×p такая, что wik =ui1·v1k+ui2·v2k+…+uin·vnk, где i= т.е. элемент i -й строки и k -го столбца матрицы произведения W равен сумме произведений элементов i -й строки матрицы U на соответствующие элементы k -го столбца матрицы V. В результате получаем А'В= Умножаем единичную матрицу на число α. По определению произведением матрицы U=(uij) размером m×n на число α называется матрица W=(wij) размером m×n такая, что wij=k· uij, где i= Таким образом, αЕ= Суммируем матрицы А'В и αЕ. По определению суммой двух матриц U=(uij) размером m×n и V=(vjj) размером m×n называется матрица W=(wij) размером m×n такая, что wij=uij+vij, где i= Окончательно получаем А'В+ αЕ= Для вычисления определителя этой матрицы воспользуемся свойством 7 определителей ([3], с. 17): определитель равен сумме произведений элементов некоторого ряда (строки или столбца) на соответствующие им алгебраические дополнения. Для разложения определителя обычно выбирают тот ряд, где есть нулевые элементы, т. к. соответствующие им слагаемые в разложении будут равны нулю. В нашем случае разложим определитель по элементам 4-й строки:
| А'В+ αЕ|=2·
+(−1+ α;)·
Определители 3-го порядка в правой части выражения представляют собой миноры элементов 4-й строки. Минор элемента (i,j) определителя есть определитель, получаемый из исходного определителя путем вычеркивания элементов i -й строки и j -го столбца. Алгебраическим дополнением элемента (i,j) определителя называется его минор, взятый со знаком «плюс», если сумма i+j − четное число, и со знаком «минус», если сумма нечетная. Вычисляя определители 3-го порядка по правилу треугольников (или Саррюса), получаем его выражение в виде многочлена четвертой степени: | А'В+ αЕ|=α4−46α2. Значения α, при которых определитель матрицы А’В+ αЕ равен нулю, представляют собой различные корни уравнения α4−46α2=0 или α2(α2−46)=0. Отсюда α1=0, α2,3=± Алгебра и геометрия: методические указания к изучению курса и контрольные задания для студентов заочной формы обучения направлений 230100.62 «Информатика и вычислительная техника» и 230400.62 «Информационные системы и технологии» (1 семестр)
Алексей Петрович Мысютин
Научный редактор Гусакова Л.А.
Редактор издательства Афонина Л.И.
Компьютерный набор Левкина А.П.
Темплан 2012 г., п. 53 Подписано в печать __.__.12 Формат 60х84 1/16 Бумага офсетная Офсетная печать. Печ. л. 1,27 Уч.-изд. л. 1,27 Т. 30 экз. Заказ Издательство Брянского государственного технического университета Брянск, бульвар 50-летия Октября, 7 Лаборатория оперативной печати БГТУ, ул. Институтская, 16.
|

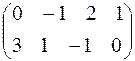 и В=
и В=  .
. .
. k=
k= 
 .
.
 .
. .
.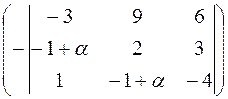 +1·
+1· 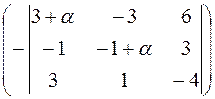 +
+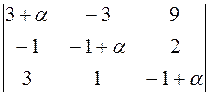 .
.



