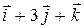Задания контрольной работы №2
1. Найти разложение вектора
2. Найти сумму координат единичного вектора
3. Даны векторы
4. Известны длины векторов Найти скалярное произведение (
5. Даны длины векторов
6. Найти объем тетраэдра АВСD.
7а. Найти значение a, при котором векторы
7б. Найти значение a, при котором векторы
8. Вычислить работу силы
Вопросы к зачету (часть 2) 1. Что называется вектором и модулем вектора? 2. Какие векторы называется равными, коллинеарными, компланарными? 3. Могут ли два вектора, имеющих равные модули, быть не равными? Если да, то чем они могут различаться? 4. Все векторы, имеющие один и тот же модуль, отложены из одной точки А пространства. Где находятся концы этих векторов? 5. Какие операции над векторами называются линейными и какие свойства этих операций? 6. Что называется базисом на прямой, на плоскости и в пространстве? 7. В каком случае векторы называются линейно зависимыми и в каком – линейно независимыми? 8. Какой базис называется ортонормированным? 9. Как определяется декартова система координат? 10.Как определяются координаты вектора через координаты его начальной и конечной точек? 11.Напишите формулы деления отрезка в данном отношении? 12.Что называется скалярным произведением двух векторов, каковы его свойства и как оно выражается через координаты векторов-сомножителей в ортонормированном базисе? 13.Напишите формулы для длины вектора, угла между двумя векторами и расстояния между двумя точками в декартовой прямоугольной системе координат. 14.Что называется векторным произведением двух векторов, каковы его свойства и как оно выражается через координаты векторов-сомножителей в ортонормированном базисе? 15.Что называется смешанным произведением трех векторов, каковы его свойства и как оно выражается через координаты векторов-сомножителей в ортонормированном базисе? 16.Как преобразуются координаты вектора при замене базиса пространства (плоскости)? 17.Какому условию должны удовлетворять координаты трех векторов, чтобы их можно было принять за базис пространства? 18.Сформулируйте условие перпендикулярности двух векторов, компланарности трех векторов. 19. Как определяется проекция вектора на заданное направление? 20. Как определяется работа постоянной силы при прямолинейном перемещении?
|

 по векторам
по векторам  , если в треугольнике АВС заданная сторона разделена точкой D в отношении m:n, считая от заданной вершины.
, если в треугольнике АВС заданная сторона разделена точкой D в отношении m:n, считая от заданной вершины.




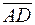



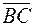
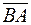


 , удовлетворяют заданным условиям.
, удовлетворяют заданным условиям. . Найти проекцию вектора
. Найти проекцию вектора  на ось вектора
на ось вектора  .
.





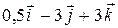




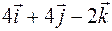
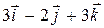









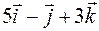



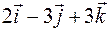



 .
. .
.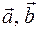 и угол между ними a. Найти площадь параллелограмма, построенного на векторах
и угол между ними a. Найти площадь параллелограмма, построенного на векторах  .
.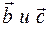 компланарны.
компланарны.

 при прямолинейном перемещении материальной точки из положения А в положение В.
при прямолинейном перемещении материальной точки из положения А в положение В.