Решение. Сначала построим таблицу значений и :Сначала построим таблицу значений
Построим эти точки в полярной системе координат. Полярная система координат состоит из начала координат
Рис. 15
Построим все точки, определенные в таблице и соединим их плавной линией
Рис. 16 Запишем уравнение рассматриваемой кривой в прямоугольной декартовой системе координат. Для этого воспользуемся формулами перехода от декартовой к полярной системе координат. Если полюс совпадает с началом координат прямоугольной декартовой системы координат, полярная ось – с осью абсцисс, то между прямоугольными декартовыми координатами
Откуда
Рис. 17 Итак, в уравнении исходной кривой
Задача №5. Построить на плоскости геометрическое место точек, определяемое неравенствами 1) 2)
|
и 
:
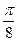
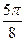
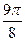
(полюса) и полярной оси 
. Координаты точки 
в полярной системе координат определяются расстоянием 
и полярными координатами 
существует следующая связь:
, 
, 
. Поэтому уравнение 
принимает вид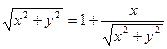 
. После преобразований получим уравнение 
.
