Решение. Для того, чтобы решить неравенство на плоскости, надо построить график линии
Для того, чтобы решить неравенство 1) Построим прямые
Рис. 18
2) Построим линию, определяемую уравнением
Рис. 19
Контрольная работа № 3 Вариант 1. Задача 1. Даны три последовательные вершины параллелограмма А(1;2), В(-1;3),С(-4;-2). Не находя координаты вершины D, найти: 6) уравнение стороны AD; 7) уравнение высоты BK, опущенной из вершины В на сторону AD; 8) длину высоты BK; 9) уравнение диагонали BD; 10) тангенс угла между диагоналями параллелограмма. Записать общие уравнения найденных прямых. Построить чертеж. Задача 2. Даны точки A(1;2;3), B(-1;3;5), C(2;0;4), D(3;-1;2). Найти: 1) общее уравнение плоскости АВС; 2) общее уравнение плоскости, проходящей через точку D параллельно плоскости АВС; 3) расстояние от точки D до плоскости ABC; 4) канонические уравнения прямой АВ; 5) канонические уравнения прямой, проходящей через точку D параллельно прямой AB; 6) общее уравнение плоскости, проходящей через точку D перпендикулярно прямой AB. Задача 3. Уравнение второго порядка Задача 4. Кривая задана в полярной системе координат уравнением Требуется: 5) найти точки, лежащие на кривой, давая 6) построить полученные точки; 7) построить кривую, соединив построенные точки (от руки или с помощью лекала); 8) составить уравнение этой кривой в прямоугольной декартовой системе координат. Задача 5. Построить на плоскости геометрическое место точек, определяемое неравенствами 1) 2)
|

 на плоскости, надо построить график линии
на плоскости, надо построить график линии  . Кривая
. Кривая  разбивает плоскость на части, в каждой из которых выражение
разбивает плоскость на части, в каждой из которых выражение  сохраняет свой знак. Выбирая пробную точку в каждой из этих частей, найдем часть плоскости, являющуюся искомым решением неравенства.
сохраняет свой знак. Выбирая пробную точку в каждой из этих частей, найдем часть плоскости, являющуюся искомым решением неравенства. и
и  , заштрихуем область, в которой
, заштрихуем область, в которой 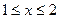 . Затем построим параболу
. Затем построим параболу 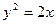 и заштрихуем область, содержащую ось симметрии параболы (расположенную внутри параболы); построим прямую
и заштрихуем область, содержащую ось симметрии параболы (расположенную внутри параболы); построим прямую  и заштрихуем область, лежащую выше прямой. Пересечение всех заштрихованных областей и определит множество точек, представляющих решение рассматриваемой системы.
и заштрихуем область, лежащую выше прямой. Пересечение всех заштрихованных областей и определит множество точек, представляющих решение рассматриваемой системы.
 . Эта линия представляет собой ту часть окружности
. Эта линия представляет собой ту часть окружности  или
или  , на которой
, на которой  . Далее построим прямую
. Далее построим прямую  (
( ). Решением рассматриваемого двойного неравенства является часть плоскости, расположенная между нижней половиной окружности
). Решением рассматриваемого двойного неравенства является часть плоскости, расположенная между нижней половиной окружности 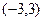 радиуса
радиуса  прямой
прямой 
 путем выделения полного квадрата привести к каноническому виду. Построить кривую, определяемую этим уравнением.
путем выделения полного квадрата привести к каноническому виду. Построить кривую, определяемую этим уравнением. .
. значения через промежуток, равный
значения через промежуток, равный 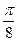 , начиная от
, начиная от  до
до  ;
; ;
;



