Угол  между двумя плоскостями
между двумя плоскостями 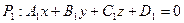 и
и  представляет собой угол между их нормальными векторами и определяется равенством
представляет собой угол между их нормальными векторами и определяется равенством

Для плоскости  координаты нормального вектора
координаты нормального вектора  определяются равенствами
определяются равенствами 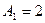 ,
,  ,
,  . Для плоскости
. Для плоскости  - равенствами
- равенствами  ,
,  ,
,  . Следовательно,
. Следовательно,  =
=  .
.
4) Составить уравнение плоскости  , проходящей через точку
, проходящей через точку  параллельно плоскости
параллельно плоскости  :
:  .
.
Решение.
Уравнение плоскости, проходящей через точку 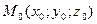 , имеет вид
, имеет вид
 (3.8)
(3.8)
Подставим в уравнение (3.8) координаты точки  :
:  .
.
Условие параллельности плоскостей  и
и  имеет вид
имеет вид
 (3.9)
(3.9)
Так как плоскости  и
и  параллельны, то в качестве нормального вектора
параллельны, то в качестве нормального вектора 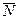 плоскости
плоскости  можно взять нормальный вектор
можно взять нормальный вектор 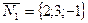 плоскости
плоскости  , т.е. в формуле (3.9) отношение
, т.е. в формуле (3.9) отношение  можно принять равным единице. Следовательно, уравнение плоскости
можно принять равным единице. Следовательно, уравнение плоскости  примет вид
примет вид  . Запишем это уравнение в общем виде:
. Запишем это уравнение в общем виде:  .
.
5) Найти расстояние от точки  до плоскости
до плоскости  :
:  .
.
Решение.
Расстояние 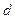 от точки
от точки 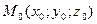 до плоскости
до плоскости  представляет собой длину перпендикуляра, опущенного из точки на плоскость, и определяется формулой
представляет собой длину перпендикуляра, опущенного из точки на плоскость, и определяется формулой
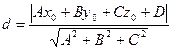 (3.10)
(3.10)
Для плоскости  координаты нормального вектора
координаты нормального вектора 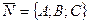 определяются равенствами
определяются равенствами 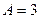 ,
, 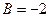 ,
, 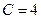 . Следовательно,
. Следовательно,  .
.
6) Составить канонические уравнения прямой, проходящей через точки  и
и  .
.
Решение.
Уравнения прямой, проходящей через точки  и
и  имеют вид
имеют вид
 (3.11)
(3.11)
Так как  ,
,  , то в силу (3.11) получим уравнения
, то в силу (3.11) получим уравнения  или
или 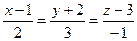 .
.
7) Найти направляющий вектор прямой  .
.

 между двумя плоскостями
между двумя плоскостями 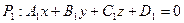 и
и  представляет собой угол между их нормальными векторами и определяется равенством
представляет собой угол между их нормальными векторами и определяется равенством
 координаты нормального вектора
координаты нормального вектора  определяются равенствами
определяются равенствами 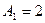 ,
,  ,
,  . Для плоскости
. Для плоскости  - равенствами
- равенствами  ,
,  ,
,  . Следовательно,
. Следовательно,  =
=  .
. , проходящей через точку
, проходящей через точку  параллельно плоскости
параллельно плоскости  :
:  .
.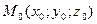 , имеет вид
, имеет вид (3.8)
(3.8) :
:  .
. и
и  имеет вид
имеет вид (3.9)
(3.9) параллельны, то в качестве нормального вектора
параллельны, то в качестве нормального вектора 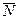 плоскости
плоскости 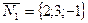 плоскости
плоскости  можно принять равным единице. Следовательно, уравнение плоскости
можно принять равным единице. Следовательно, уравнение плоскости  . Запишем это уравнение в общем виде:
. Запишем это уравнение в общем виде:  .
. до плоскости
до плоскости  .
.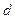 от точки
от точки  представляет собой длину перпендикуляра, опущенного из точки на плоскость, и определяется формулой
представляет собой длину перпендикуляра, опущенного из точки на плоскость, и определяется формулой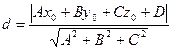 (3.10)
(3.10)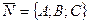 определяются равенствами
определяются равенствами 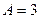 ,
, 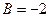 ,
, 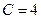 . Следовательно,
. Следовательно,  .
. и
и  .
. и
и  имеют вид
имеют вид (3.11)
(3.11) или
или 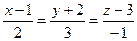 .
. .
.


