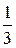Так же, как и в рассмотренных выше примерах, ничего определённого о
пределе частного
Чтобы вычислить данный предел (или, как говорят, раскрыть неопределённость), разделим числитель и знаменатель дроби на
Так как
Пример 7. Найти Этот предел также является неопределённостью вида
Пример 8. Найти
Так как
то
Однако подчеркнём, что знаменатель не равен нулю, а лишь стремится к нему, неограниченно уменьшаясь по абсолютной величине с ростом Поэтому
Примеры 6-8 позволяют сформулировать общее правило вычисления пределов вида где
Это правило верно не только для рационального выражения R(x), но и для отношения иррациональных функций. Пример 9. Найти
Предел является неопределённостью вида = Упражнения. Вычислить пределы функций:
1)
4) 7)
10)
13)
16)
19)
22)
25)
28)
31)
Ответы
Бесконечно малые функции.
|

 сразу сказать нельзя, если
сразу сказать нельзя, если  .
. - старшую степень аргумента:
- старшую степень аргумента: .
. , то, используя теоремы 1,2,3,5, получаем
, то, используя теоремы 1,2,3,5, получаем
 =
=  .
. .
. . Чтобы раскрыть её, разделим числитель и знаменатель дроби на
. Чтобы раскрыть её, разделим числитель и знаменатель дроби на  - старшую степень аргумента:
- старшую степень аргумента: .
. .
. - старшая степень аргумента, поэтому
- старшая степень аргумента, поэтому .
.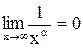 при всех
при всех 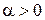 ,
, ,
, 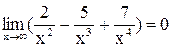 .
.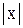 .
.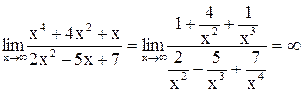 .
. ,
, .
. 
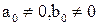 .
. .
. .
.
 .
. . 2)
. 2)  . 3)
. 3)  .
. . 5)
. 5)  . 6)
. 6)  .
. . 8)
. 8)  . 9)
. 9)  .
. . 11)
. 11)  . 12)
. 12)  .
. . 14)
. 14)  . 15)
. 15) 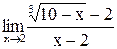 .
. . 17)
. 17)  . 18)
. 18)  .
. . 20)
. 20)  . 21)
. 21)  .
.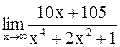 . 23)
. 23)  . 24)
. 24)  .
. . 26)
. 26)  . 27)
. 27)  .
. . 29)
. 29)  . 30)
. 30)  .
. . 32)
. 32)  .
.