Введём понятие одностороннего (правого или левого) предела функции в данной точке a.
Определение 1. Число b называется правым (левым) пределом функции  при
при  , если для любого числа
, если для любого числа 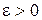 можно указать такой интервал
можно указать такой интервал 
 ,
,  , что всюду внутри этого интервала будет выполняться неравенство
, что всюду внутри этого интервала будет выполняться неравенство  .
.
Обозначаются односторонние пределы в точке x=a так:
 или
или  - правый предел
- правый предел
 или
или  - левый предел.
- левый предел.
В качестве примера рассмотрим ещё раз функцию (рис. 7) 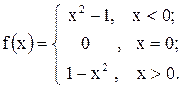
 В пункте 1 было отмечено, что
В пункте 1 было отмечено, что  не существует, но вместе с тем очевидно, что если xcтремится к нулю, оставаясь отрицательным (то есть слева), то
не существует, но вместе с тем очевидно, что если xcтремится к нулю, оставаясь отрицательным (то есть слева), то 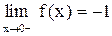 . А если x стремится к нулю справа (оставаясь положительным), то
. А если x стремится к нулю справа (оставаясь положительным), то 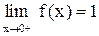 .
. 
Геометрическая иллюстрация этих 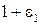 утверждений – на рис. 7. Зададим
утверждений – на рис. 7. Зададим 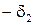
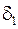
 , тогда для всех
, тогда для всех  -1 0 1 x
-1 0 1 x
выполняется неравенство 
 ,
,  .
. 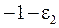
Точно также для произвольного 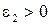 при всех
при всех  имеет Рис. 7
имеет Рис. 7
место неравенство  или
или  .
.
Пример. Вычислить односторонние пределы функции  в точках
в точках 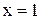 и
и  .
.
Пусть  (справа), тогда
(справа), тогда  и
и  .
.
Следовательно,  ,
,  .
.
Если  (слева), то
(слева), то  и
и  , поэтому
, поэтому
 ,
, 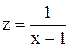 . Очевидно, что
. Очевидно, что  не существует. Если
не существует. Если
 , то
, то  , но и при
, но и при 
 .
.
Поэтому 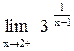 =
= 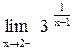 =
= 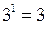 . Связь между односторонними пределами и пределом функции в точке устанавливает следующая теорема.
. Связь между односторонними пределами и пределом функции в точке устанавливает следующая теорема.
Теорема. Если функция 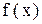 имеет в точке
имеет в точке 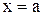 как правый, так и левый пределы и если эти односторонние пределы равны одному и тому же числу
как правый, так и левый пределы и если эти односторонние пределы равны одному и тому же числу  , то эта функция имеет в точке
, то эта функция имеет в точке 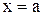 предел, равный
предел, равный  .
.
Наоборот, если  , то
, то 
Для односторонних пределов верны все теоремы п. 2.

 при
при  , если для любого числа
, если для любого числа 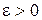 можно указать такой интервал
можно указать такой интервал 
 ,
,  , что всюду внутри этого интервала будет выполняться неравенство
, что всюду внутри этого интервала будет выполняться неравенство  .
. или
или  - правый предел
- правый предел или
или  - левый предел.
- левый предел.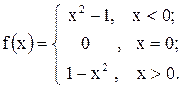
 В пункте 1 было отмечено, что
В пункте 1 было отмечено, что  не существует, но вместе с тем очевидно, что если xcтремится к нулю, оставаясь отрицательным (то есть слева), то
не существует, но вместе с тем очевидно, что если xcтремится к нулю, оставаясь отрицательным (то есть слева), то 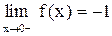 . А если x стремится к нулю справа (оставаясь положительным), то
. А если x стремится к нулю справа (оставаясь положительным), то 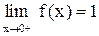 .
. 
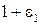 утверждений – на рис. 7. Зададим
утверждений – на рис. 7. Зададим 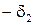
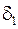
 , тогда для всех
, тогда для всех  -1 0 1 x
-1 0 1 x
 ,
,  .
. 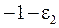
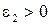 при всех
при всех  имеет Рис. 7
имеет Рис. 7 или
или  .
. в точках
в точках 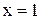 и
и  .
. (справа), тогда
(справа), тогда  и
и  .
. ,
,  .
. (слева), то
(слева), то  и
и  , поэтому
, поэтому ,
, 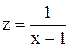 . Очевидно, что
. Очевидно, что  не существует. Если
не существует. Если , то
, то  , но и при
, но и при 
 .
.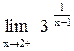 =
= 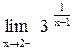 =
= 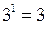 . Связь между односторонними пределами и пределом функции в точке устанавливает следующая теорема.
. Связь между односторонними пределами и пределом функции в точке устанавливает следующая теорема.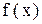 имеет в точке
имеет в точке 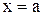 как правый, так и левый пределы и если эти односторонние пределы равны одному и тому же числу
как правый, так и левый пределы и если эти односторонние пределы равны одному и тому же числу  , то эта функция имеет в точке
, то эта функция имеет в точке  , то
, то 



