функции в точке, нетрудно доказать теорему об арифметических действиях над непрерывными функциями.
Теорема. Пусть функции  ,
, 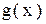 непрерывны в точке
непрерывны в точке 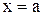 . Тогда функции
. Тогда функции  ±
± 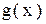 ,
,  ·
· 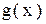 и
и 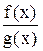 непрерывны в этой точке (последняя при
непрерывны в этой точке (последняя при 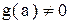 ).
).
Все элементарные функции, то есть такие, которые можно задать одним анали-
тическим выражением, полученным из простейших элементарных функций с помощью четырёх арифметических действий и операции составления сложной функции, последовательно применённых конечное число раз, непрерывны на области определения, то есть в каждой точке, в которой определены. К простей-шим элементарным функциям относятся степенная, показательная, логарифми-ческая, тригонометрические и обратные тригонометрические функции.
Функции 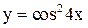 ,
, 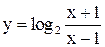 ,
, 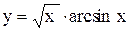 ,
, 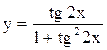 и т.д. - элементарные. Каждая из них непрерывна всюду, где определена.
и т.д. - элементарные. Каждая из них непрерывна всюду, где определена.
Как было сказано выше, точка 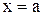 называется точкой разрыва
называется точкой разрыва
функции 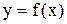 , если
, если 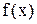 в этой точке не является непрерывной.
в этой точке не является непрерывной.
Разрывы классифицируются следующим образом:
1) точка 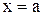 называется точкой устранимогоразрыва, если существует
называется точкой устранимогоразрыва, если существует  , но либо
, но либо 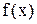 не определена в этой точке, либо
не определена в этой точке, либо 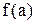
 . Если положить
. Если положить 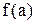
 , то функция
, то функция 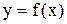 станет непрерывной в точке
станет непрерывной в точке 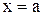 , т. е. разрыв будет устранён.
, т. е. разрыв будет устранён.
Пример 1. Исследовать на непрерывность функцию 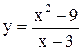 .
.
Функция 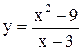 - элементарная, значит, непрерывна всюду, где определена, именно во всех точках действительной оси, кроме x = 3. Заметим, что при
- элементарная, значит, непрерывна всюду, где определена, именно во всех точках действительной оси, кроме x = 3. Заметим, что при 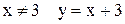 , поэтому
, поэтому 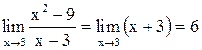 (см.п.1), т. е. существует
(см.п.1), т. е. существует 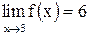 , но
, но 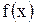 не определена при
не определена при 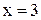 . Это означает, что функция
. Это означает, что функция 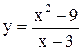 имеет в точке
имеет в точке 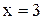 устранимый разрыв. Функция, определённая таким образом:
устранимый разрыв. Функция, определённая таким образом: 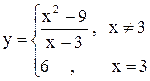 - является непрерывной для всех
- является непрерывной для всех 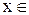 R.
R.
Пример 2. Исследовать на непрерывность функцию 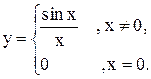
Функция 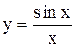 определена, а значит, непрерывна всюду, за исключением точки
определена, а значит, непрерывна всюду, за исключением точки 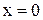 . В п. 3 было отмечено, что
. В п. 3 было отмечено, что 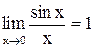 , но
, но 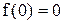 , поэтому точка
, поэтому точка 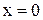 - точка устранимого разрыва. Доопределив функцию
- точка устранимого разрыва. Доопределив функцию 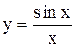 при
при 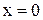 другим образом, полагая
другим образом, полагая 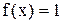 , устраним разрыв и получим функцию, непрерывную при всех
, устраним разрыв и получим функцию, непрерывную при всех  .
.
2) точка 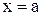 называется точкой разрыва I рода функции
называется точкой разрыва I рода функции 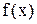 , если в этой точке функция имеет конечные, но не равные друг другу односторонние пределы:
, если в этой точке функция имеет конечные, но не равные друг другу односторонние пределы: 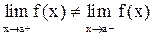 . Величина ½
. Величина ½ 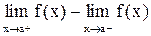 ½ называется скачком функции в точке
½ называется скачком функции в точке 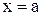 .
.
Пример 3. Исследовать на непрерывность функцию (рис. 5) 
Так как  , а
, а 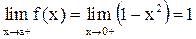 ,
,
то точка 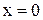 является для данной функции точкой разрыва I рода.
является для данной функции точкой разрыва I рода.
Пример 4. Исследовать на непрерывность функцию 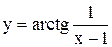 .
.
 Данная функция определена, а значит, непрерывна при всех
Данная функция определена, а значит, непрерывна при всех 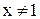 . Вычислим односторонние пределы
. Вычислим односторонние пределы 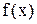 в этой точке. Вначале отметим, что
в этой точке. Вначале отметим, что 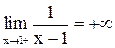 , а
, а 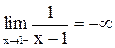 . Следовательно, y
. Следовательно, y
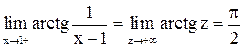
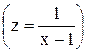 .
. 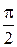
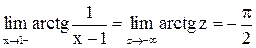 . 1 x
. 1 x
Это означает, что точка 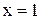
является точкой разрыва I рода 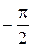
для функции 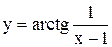 (рис. 9). Рис. 9
(рис. 9). Рис. 9
3) точка 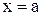 называется точкой разрыва II рода функции
называется точкой разрыва II рода функции 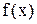 , если в этой точке функция
, если в этой точке функция 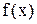 не имеет, по крайней мере, одного из односторонних пределов или хотя бы один из односторонних пределов бесконечен.
не имеет, по крайней мере, одного из односторонних пределов или хотя бы один из односторонних пределов бесконечен.
Пример 5. Исследовать на непрерывность функцию 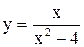 .
.
В точках  данная функция не определена. Чтобы исследовать характер разрыва функции в этих точках, вычислим односторонние пределы. Пусть
данная функция не определена. Чтобы исследовать характер разрыва функции в этих точках, вычислим односторонние пределы. Пусть  , тогда разность
, тогда разность 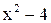 стремится к 0, оставаясь положительной, поэтому
стремится к 0, оставаясь положительной, поэтому 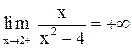 . Аналогично
. Аналогично  . Следовательно, точка
. Следовательно, точка 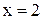 - точка разрыва II рода. Пусть
- точка разрыва II рода. Пусть 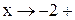 . Тогда
. Тогда 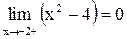 , и
, и  , следовательно,
, следовательно,  , а
, а 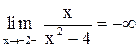 , то есть точка
, то есть точка 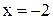 - также точка разрыва II рода функции
- также точка разрыва II рода функции 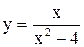 .
.
Пример 6. Исследовать на непрерывность функцию 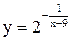 .
.
Эта функция непрерывна в любой точке 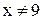 . Прежде чем вычислить
. Прежде чем вычислить 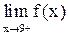 и
и  , заметим, что
, заметим, что 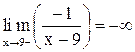 , а
, а 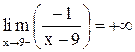 . Тогда получим
. Тогда получим 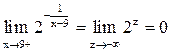 ;
; 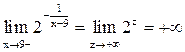 . Таким образом, левый предел
. Таким образом, левый предел 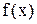 в точке
в точке 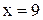 бесконечен и, значит,
бесконечен и, значит, 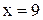 является точкой разрыва II рода слева.
является точкой разрыва II рода слева.
Пример 7. Исследовать на непрерывность функцию  .
.
Функция не определена при 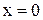 . Обозначим
. Обозначим 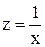 , тогда
, тогда 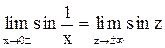 . Этот предел, как было отмечено в п.1, не существует, поэтому точка
. Этот предел, как было отмечено в п.1, не существует, поэтому точка 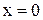 является для функции
является для функции  точкой разрыва II рода.
точкой разрыва II рода.
Упражнения. Найти точки разрыва функции, исследовать их характер, в случае устранимого разрыва доопределить функцию по непрерывности:
54) 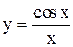 . 55)
. 55) 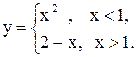 56)
56) 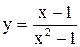 .
.
57) 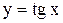 . 58)
. 58) 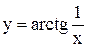 . 59)
. 59) 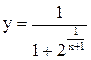 .
.
60) 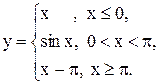 61)
61) 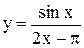 . 62)
. 62) 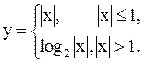
63)  64)
64) 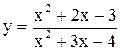 . 65)
. 65) 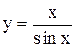 .
.
66)  . 67)
. 67) 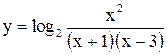 . 68)
. 68)  . 69)
. 69) 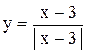 .
.
70) 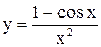 . 71)
. 71) 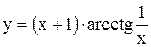 . 72)
. 72) 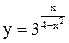 .
.
Ответы
54. 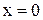 - разрыв II рода. 55.
- разрыв II рода. 55. 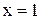 - устранимый разрыв, y(1)=1. 56.
- устранимый разрыв, y(1)=1. 56. 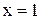 - устранимый разрыв, y(1) =
- устранимый разрыв, y(1) =  . 57.
. 57.  - разрыв II рода. 58.
- разрыв II рода. 58. 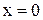 - разрыв I рода. 59.
- разрыв I рода. 59. 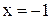 - разрыв I рода. 60. Функция непрерывна. 61.
- разрыв I рода. 60. Функция непрерывна. 61. 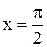 - разрыв II рода.
- разрыв II рода.
62. 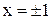 -разрыв I рода. 63.
-разрыв I рода. 63. 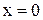 - разрыв II рода справа.
- разрыв II рода справа.
64. 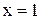 - устранимый разрыв, y(1) = 0,8; 65.
- устранимый разрыв, y(1) = 0,8; 65. 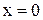 - устранимый разрыв, y(0)=1;
- устранимый разрыв, y(0)=1;
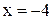 - разрыв II рода.
- разрыв II рода. 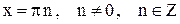 - разрыв II
- разрыв II
рода.
66. 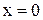 - разрыв II рода. 67.
- разрыв II рода. 67. 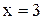 - разрыв II рода справа;
- разрыв II рода справа;
68. 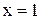 - разрыв II рода.
- разрыв II рода. 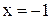 - разрыв II рода слева.
- разрыв II рода слева.
69. 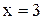 - разрыв I рода. 70.
- разрыв I рода. 70. 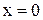 - устранимый разрыв, y(0)=0,5.
- устранимый разрыв, y(0)=0,5.
71. 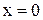 - разрыв I рода. 72.
- разрыв I рода. 72.  -разрыв II рода.
-разрыв II рода.

 ,
, 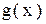 непрерывны в точке
непрерывны в точке 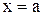 . Тогда функции
. Тогда функции 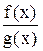 непрерывны в этой точке (последняя при
непрерывны в этой точке (последняя при 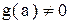 ).
).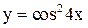 ,
, 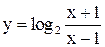 ,
, 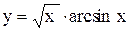 ,
, 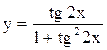 и т.д. - элементарные. Каждая из них непрерывна всюду, где определена.
и т.д. - элементарные. Каждая из них непрерывна всюду, где определена.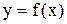 , если
, если 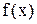 в этой точке не является непрерывной.
в этой точке не является непрерывной. , но либо
, но либо 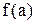
 . Если положить
. Если положить  , то функция
, то функция 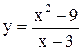 .
.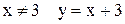 , поэтому
, поэтому 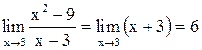 (см.п.1), т. е. существует
(см.п.1), т. е. существует 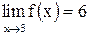 , но
, но 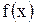 не определена при
не определена при 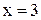 . Это означает, что функция
. Это означает, что функция 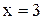 устранимый разрыв. Функция, определённая таким образом:
устранимый разрыв. Функция, определённая таким образом: 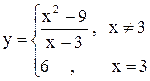 - является непрерывной для всех
- является непрерывной для всех 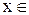 R.
R.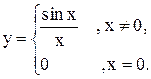
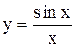 определена, а значит, непрерывна всюду, за исключением точки
определена, а значит, непрерывна всюду, за исключением точки 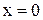 . В п. 3 было отмечено, что
. В п. 3 было отмечено, что 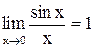 , но
, но 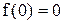 , поэтому точка
, поэтому точка 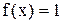 , устраним разрыв и получим функцию, непрерывную при всех
, устраним разрыв и получим функцию, непрерывную при всех  .
.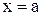 называется точкой разрыва I рода функции
называется точкой разрыва I рода функции 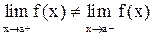 . Величина ½
. Величина ½ 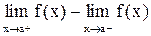 ½ называется скачком функции в точке
½ называется скачком функции в точке 
 , а
, а 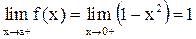 ,
,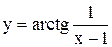 .
. Данная функция определена, а значит, непрерывна при всех
Данная функция определена, а значит, непрерывна при всех 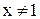 . Вычислим односторонние пределы
. Вычислим односторонние пределы 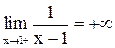 , а
, а 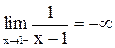 . Следовательно, y
. Следовательно, y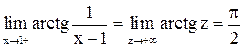
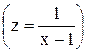 .
. 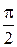
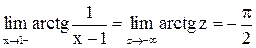 . 1 x
. 1 x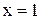
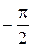
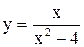 .
. данная функция не определена. Чтобы исследовать характер разрыва функции в этих точках, вычислим односторонние пределы. Пусть
данная функция не определена. Чтобы исследовать характер разрыва функции в этих точках, вычислим односторонние пределы. Пусть  , тогда разность
, тогда разность 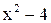 стремится к 0, оставаясь положительной, поэтому
стремится к 0, оставаясь положительной, поэтому 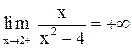 . Аналогично
. Аналогично  . Следовательно, точка
. Следовательно, точка 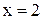 - точка разрыва II рода. Пусть
- точка разрыва II рода. Пусть 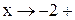 . Тогда
. Тогда 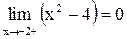 , и
, и  , следовательно,
, следовательно,  , а
, а 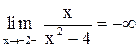 , то есть точка
, то есть точка 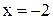 - также точка разрыва II рода функции
- также точка разрыва II рода функции 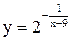 .
.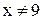 . Прежде чем вычислить
. Прежде чем вычислить 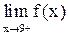 и
и  , заметим, что
, заметим, что 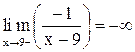 , а
, а 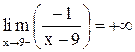 . Тогда получим
. Тогда получим 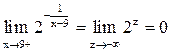 ;
; 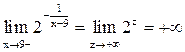 . Таким образом, левый предел
. Таким образом, левый предел 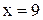 бесконечен и, значит,
бесконечен и, значит,  .
.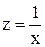 , тогда
, тогда 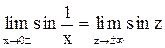 . Этот предел, как было отмечено в п.1, не существует, поэтому точка
. Этот предел, как было отмечено в п.1, не существует, поэтому точка 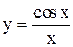 . 55)
. 55) 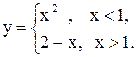 56)
56) 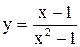 .
.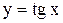 . 58)
. 58) 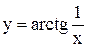 . 59)
. 59) 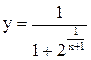 .
.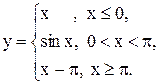 61)
61) 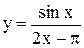 . 62)
. 62) 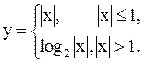
 64)
64) 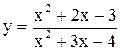 . 65)
. 65) 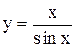 .
. . 67)
. 67) 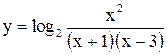 . 68)
. 68)  . 69)
. 69) 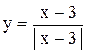 .
.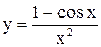 . 71)
. 71) 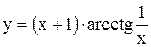 . 72)
. 72) 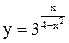 .
. . 57.
. 57.  - разрыв II рода. 58.
- разрыв II рода. 58. 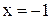 - разрыв I рода. 60. Функция непрерывна. 61.
- разрыв I рода. 60. Функция непрерывна. 61. 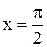 - разрыв II рода.
- разрыв II рода.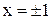 -разрыв I рода. 63.
-разрыв I рода. 63. 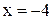 - разрыв II рода.
- разрыв II рода. 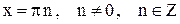 - разрыв II
- разрыв II


