Принцип замены бесконечно малых
Определение 1. Функция Пример 1. Функция
Функция Пусть
Определение 2. Бесконечно малые в точке называются эквивалентными, если Эквивалентность обозначается так:
Пример 2. Функции Пример 3. Функции
При этом
Раскрытие неопределённости вида
Если существует
причём
Это утверждение называется принципом замены бесконечно малых.
Можно показать, что
Поэтому при
sin t ~ t, tg t ~ t, arcsin t ~ t, arctg t ~ t
Замечание. Равенство Пример 4. Найти Заменим числитель и знаменатель дроби эквивалентными б.м.: tg 3x ~ 3x, sin 4x ~ 4x. Тогда получим
Пример 5. Найти Так как ( то
Пример 6. Найти Заметим, что
Отсюда
Пример 7. Найти
Теперь имеем
|
называется бесконечно малой функцией (или просто бесконечно малой) в точке 
(или при 
), если 
.
- бесконечно мала (б.м.) в точках
и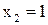 
, так как 
и 
.
б.м. при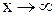 
, так как 
.
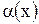, то есть функции 
и 
- б.м. в точке 
.
и 
б.м. при 
, кроме того, 
. Значит, 
.
, 
, 
- б.м. при 
.
, так как 
. Однако бесконечно малые 
.
во многих случаях упрощает следующее утверждение:
и 
при 
, то существует и 
,
.
, 
, 
, 
, 
,
, 
.
~ t, ln (1+t)~ t, 
~ 
.
называется первым замечательным пределом.
.
.
.
) ~ 
, 
~ (
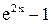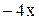) при x®0,
.
.
, поэтому
= 
~ 
~ 
, а 
~ 
при 
.
.
.
, но, чтобы заменить бесконечно малые на эквивалентные им, введём другую переменную: 
или 
. Тогда 
; 
.
.
