Распределение доходов населения России в январе - сентябре 1995г.
Для расчета коэффициента Джини воспользуемся итоговыми данными граф 4 и 6 таблицы 10.4: G = 1 - 2
Такой же результат мы получим, выполнив расчеты в процентах: G = 120 - 0,4 (5,5 + 15,7 + 30,9 + 53,3 + 100,0) = 37,8%.
Второй способ расчета проще, однако, исходная формула незаменима в тех случаях, когда имеются неравные группы по объему совокупности (в нашем примере - по численности населения). Используя данные графы 7 таблицы 10.4 определим коэффициент Лоренца:
L =
Оба коэффициента указывают на относительно высокую степень концентрации доходов населения.
Если под концентрацией понимается степень неравномерности распределения изучаемого признака, не связанная ни с объемом совокупности, ни с численностью отдельных групп, то централизация означает сосредоточение объема признака у отдельных единиц (объема продукции данного вида на отдельных предприятиях, капитала в отдельных банках и т.п.). Обобщающий показатель централизации имеет следующий вид:
где M - объем признака всей совокупности. Максимальное значение, равное 1, данный коэффициент достигает лишь в том случае, когда совокупность состоит только из одной единицы, обладающей всем объемом признака. Минимальное значение коэффициента приближается к нулю, но никогда его не достигает.
Рассмотрим следующий пример. Предположим, выпуск продукции А сконцентрирован на 5 предприятиях, расположенных в трех районах области (табл. 10.5.):
Таблица 10.5
Вычислим показатель централизации производства данного вида продукции:
Рассчитанная величина свидетельствует о высокой степени централизации. Отметим, что аналитическая ценность показателей концентрации и централизации повышается при проведении сравнений во временном или территориальном аспектах.
|





 0,4108 +0,2 = 0,378 или 37,8%.
0,4108 +0,2 = 0,378 или 37,8%.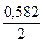 = 0,291 или 29,1%.
= 0,291 или 29,1%. , (10.15)
, (10.15)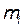 - значение признака i-ой единицы совокупности;
- значение признака i-ой единицы совокупности;



