Частные показатели структурных сдвигов
Анализ структуры и ее изменений базируется на относительных показателях структуры - долях или удельных весах, представляющих собой соотношения размеров частей и целого. При этом как частные, так и обобщающие показатели структурных сдвигов могут отражать либо «абсолютное» изменение структуры в процентных пунктах или долях единицы (кавычки показывают, что данные показатели являются абсолютными по методологии расчета, но не по единицам измерения), либо ее относительное изменение в процентах или коэффициентах.
«Абсолютный» прирост удельного веса i-ой части совокупности показывает, на сколько процентных пунктов возросла или уменьшилась данная структурная часть в j-ый период по сравнению с (j-1) периодом:[5]
где
Знак прироста показывает направление изменения удельного веса данной структуры части («+» - увеличение, «-» - уменьшение), а его значение - конкретную величину этого изменения. Темп роста удельного веса представляет собой отношение удельного веса i-ой части в j-ый период времени к удельному весу той же части в предшествующий период:
Темпы роста удельного веса выражаются в процентах и всегда являются положительными величинами. Однако, если в совокупности имели место какие-либо структурные изменения, часть темпов роста будет больше 100%, а часть - меньше. Рассчитаем частные показатели структурных сдвигов по данным о распределении коммерческих банков по размеру объявленного уставного фонда (табл. 10.1.): Таблица 10.1
Как следует из данных таблицы 10.1, наиболее существенно в «абсолютном» выражении изменился удельный вес банков с уставным фондом до 1 млрд. руб. - снизился на 20,2 процентного пункта. В относительном выражении наиболее сильно (в 3 раза) выросла доля банков с уставным фондом свыше 5 млрд. руб.
Мы рассмотрели показатели структурных сдвигов за один интервал между двумя периодами. Если же изучаемая структура представлена данными за три и более периодов, появляется необходимость в динамическом осреднении приведенных выше показателей, т.е. в расчете средних показателей структурных сдвигов.
Средний «абсолютный» прирост удельного веса i-ой структурной части показывает, на сколько процентных пунктов в среднем за какой-либо период (день, неделю, месяц, год и т.п.) изменяется данная структурная часть:
где n - число осредняемых периодов.
Сумма средних «абсолютных» приростов удельных весов всех k структурных частей совокупности, также как и сумма их приростов за один временной интервал, должна быть равна нулю. Средний темп роста удельного веса характеризует среднее относительное изменение удельного веса i-ой структурной части за n периодов, и рассчитывается по формуле средней геометрической:
Подкоренное выражение этой формулы представляет собой последовательное произведение цепных темпов роста удельного веса за все временные интервалы. После проведения несложных алгебраических преобразований данная формула примет следующий вид:
Для иллюстрации этих формул воспользуемся приведенным выше примером (таблица 10.1). Рассчитаем средний месячный прирост (в данном случае - снижение) удельного веса банков 1-ой группы:
По этой же группе определим средний месячный темп роста удельного веса:
Мы получили, что удельный вес банков данной группы в среднем ежемесячно снижался на 1,8 процентного пункта или на 3,3% (96,7%-100%).
При анализе структуры исследуемого объекта или явления за ряд периодов также можно определить средний удельный вес каждой i-ой части за весь рассматриваемый временной интервал. Однако для его расчета одних лишь относительных данных об удельных весах структурных частей недостаточно, необходимо располагать еще и информацией о размерах этих частей в абсолютном выражении. Используя эти данные, средний удельный вес любой i-ой структурной части можно определить по формуле:
где
Проиллюстрируем эту формулу следующим примером. По данным первичного рынка государственных краткосрочных облигаций (ГКО) и облигаций федерального займа (ОФЗ) в третьем квартале 1995г. определим средний удельный вес ценных бумаг каждого вида в общем объеме выручки от их реализации (табл. 10.2.):
Таблица 10.2
Определим средний удельный вес выручки от продажи ГКО в общем объеме выручки от реализации государственных ценных бумаг:
Рассчитаем средний удельный вес выручки от продажи ОФЗ:
Итак, в августе-сентябре 1995г. на долю ГКО в среднем ежемесячно приходилось 94,3% общего объема выручки от реализации государственных ценных бумаг, на долю ОФЗ - только 5,7%.
|

 , (10.1)
, (10.1) - удельный вес (доля) i-ой части совокупности в j-ый период;
- удельный вес (доля) i-ой части совокупности в j-ый период; - удельный вес (доля) i-ой части совокупности в (j-1)-ый период.
- удельный вес (доля) i-ой части совокупности в (j-1)-ый период. (10.2)
(10.2)



 , (10.3)
, (10.3) (10.4)
(10.4) (10.5)
(10.5)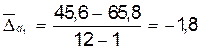 проц. пункта.
проц. пункта.
 , (10.6)
, (10.6) - величина i-ой структурной части в j- период времени в абсолютном выражении.
- величина i-ой структурной части в j- период времени в абсолютном выражении. в % к итогу
в % к итогу 
 в % к итогу
в % к итогу 
 .
. .
.


