За 1980-1995 гг. методом скользящей средней
Недостаток метода простой скользящей средней состоит в том, что сглаженный ряд динамики сокращается ввиду невозможности получить сглаженные уровни для начала и конца ряда. Этот недостаток устраняется применением метода аналитического выравнивания для анализа основной тенденции. Аналитическое выравнивание предполагает представление уровней данного ряда динамики в виде функции времени - y=f(t). Для отображения основной тенденции развития явлений во времени применяются различные функции: полиномы степени, экспоненты, логистические кривые и другие виды.
Полиномы имеют следующий вид: полином первой степени полином второй степени полином третьей степени полином n-ой степени
Здесь а0; а1; а2;... аn - параметры полиномов, t - условное обозначение времени. В статистической практике параметры полиномов невысокой степени иногда имеют конкретную интерпретацию характеристик динамического ряда. Так, параметр а0 трактуется как характеристика средних условий ряда динамики, параметры а1, а2, а3 - как изменения ускорения.
В статистике выработано правило выбора степени полинома модели развития, основанное на определении величин конечных разностей уровней динамических рядов. Согласно этому правилу полином первой степени (прямая) применяется как модель такого ряда динамики, у которого первые разности (абсолютные приросты) постоянны, полиномы второй степени - для отражения ряда динамики с постоянными вторыми разностями (ускорениями), полиномы третьей степени - с постоянными третьими разностями и т.д.
После выбора вида уравнения необходимо определить параметры уравнения. Самый распространенный способ определения параметров уравнения - это метод наименьших квадратов.
Суть данного метода изложена в главе 8. Согласно этому методу, для нахождения параметров полинома р-й степени необходимо решить систему так называемых нормальных уравнений:
где n - число членов в ряду динамики: t=1,2,...,n
Система 9.16, состоящая из «р» уравнений, содержит в качестве известных величин
Системы для расчета параметров полиномов невысоких степеней намного проще. Обозначим последовательные параметры полиномов как а0, а1, а2. Тогда системы нормальных уравнений для оценивания параметров прямой
для параболы второго порядка (yt=a0+a1t+a2t2):
Решение системы (9.17) относительно искомых параметров а0 и а1 дает:
В статической практике применяется упрощенный расчет параметров уравнений, который заключается в переносе начала координат в середину ряда динамики. В этом случае упрощаются сами нормальные уравнения, кроме того уменьшаются абсолютные значения величин, участвующих в расчете. В самом деле, если до переноса начала координат t было равно 1,2,3,...,n, то после переноса t=...-4,-3,-2,-1,0,1,2,3,4,..., если число членов ряда нечетное. Если же число членов ряда четное, то t=...,-5,-3,-1,1,3,5,... Следовательно, St и все Stp у которых «р» - нечетное число, равны 0. Таким образом, все члены уравнений, содержащие St с такими степенями могут быть исключены. Системы нормальных уравнений теперь упрощаются для прямой:
для параболы второго порядка:
Решая системы (9.19), (9.20) относительно неизвестных параметров, получим величины параметров соответствующих полиномов. Параметр а1 выражает начальную скорость роста, а коэффициент а2 - постоянную скорость изменения прироста.
При сглаживании ряда динамики по показательной кривой (yt=a0a1t) для определения параметров применяется метод наименьших квадратов к логарифмам исходных данных. Так, для нахождения параметров показательной функции необходимо решить следующую систему уравнений:
Если St=0, то параметры уравнения lga0 и lga1 находим по формулам: Рассмотрим следующий пример. Необходимо определить основную тенденцию ряда динамики урожайности зерновых культур в хозяйстве за 1981-1995 гг. по следующим данным (см. табл. 9.7). Начнем определение тенденции с самого простого полинома-уравнение прямой (9.19). Решая систему нормальных уравнений, получим искомые параметры: a0=14,8; a1=0,17, а само уравнение запишется следующим образом
Таблица 9.7 Динамика урожайности зерновых культур в хозяйстве и определение параметров уравнения методом наименьших квадратов
|



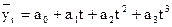

 (9.16)
(9.16) , то есть суммы наблюдаемых значений уровней динамического ряда, умноженные на показатели времени в степени 0,1,2,...,р и неизвестных величин aj. Решение этой системы относительно a0, a1,...,ap и дает искомые значения параметров.
, то есть суммы наблюдаемых значений уровней динамического ряда, умноженные на показатели времени в степени 0,1,2,...,р и неизвестных величин aj. Решение этой системы относительно a0, a1,...,ap и дает искомые значения параметров. (9.17)
(9.17) (9.18)
(9.18)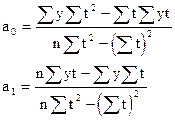
 (9.19)
(9.19) (9.20)
(9.20)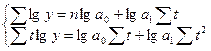 (9.21)
(9.21) ;
;  .
. что выражает тенденцию динамики урожайности зерновых культур в 1981-1995 гг., т.е. в течение исследуемого периода урожайность зерновых культур в хозяйстве увеличивалась в среднем на 0,17 ц. с га в год.
что выражает тенденцию динамики урожайности зерновых культур в 1981-1995 гг., т.е. в течение исследуемого периода урожайность зерновых культур в хозяйстве увеличивалась в среднем на 0,17 ц. с га в год.


