Пример 4. Покажем расчет дисперсии для интервального ряда на данных о распределении посевной площади колхоза по урожайности пшеницы: Урожайность пшеницыПокажем расчет дисперсии для интервального ряда на данных о распределении посевной площади колхоза по урожайности пшеницы:
Средняя арифметическая равна:
Исчислим дисперсию:
Расчет дисперсии по формуле Техника вычисления дисперсии сложна, а при больших значениях вариант и частот может быть громоздкой. Расчеты можно упростить, используя свойства дисперсии. Свойства дисперсии. - Уменьшение или увеличение весов (частот) варьирующего признака в определенное число раз дисперсии не изменяет. - Уменьшение или увеличение каждого значения признака на одну и ту же постоянную величину А дисперсии не изменяет. - Уменьшение или увеличение каждого значения признака в какое-то число раз к соответственно уменьшает или увеличивает дисперсию в Дисперсия признака относительно произвольной величины всегда больше дисперсии относительно средней арифметической на квадрат разности между средней и произвольной величиной: Каждое свойство при расчете дисперсии может быть применено самостоятельно или в сочетании с другими. Порядок расчета дисперсии простой: 1) определяют среднюю арифметическую 2) возводят в квадрат среднюю арифметическую 3) возводят в квадрат каждую варианту ряда 4) находим сумму квадратов вариант 5) делят сумму квадратов вариант на их число, т.е. определяют средний квадрат 6) определяют разность между средним квадратом признака и квадратом средней
|
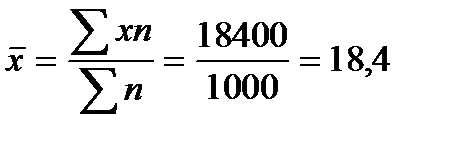ц с 1га.
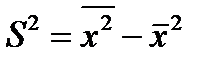по индивидуальным данным и в рядах распределения.
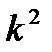раз, а среднее квадратическое отклонение - в к раз.
. Если А равна нулю, то приходим к следующему равенству: 
, т.е. дисперсия признака равна разности между средним квадратом значений признака и квадратом средней.
;
;
;
;
;
.
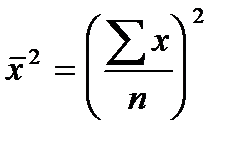