4.25. Волновая функция, описывающая движение электрона в основном состоянии атома водорода, имеет вид: 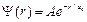 , где
, где  – нормировочный коэффициент волновой функции,
– нормировочный коэффициент волновой функции, 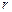 – расстояние электрона от ядра,
– расстояние электрона от ядра, 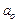 – первый боровский радиус. Определить наиболее вероятное расстояние электрона от ядра в основном состоянии. [
– первый боровский радиус. Определить наиболее вероятное расстояние электрона от ядра в основном состоянии. [ 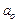 ].
].
4.26. Волновая функция, описывающая движение микрочастицы, имеет вид  , где
, где  – нормировочный коэффициент волновой функции,
– нормировочный коэффициент волновой функции, 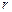 – расстояние этой частицы до силового центра,
– расстояние этой частицы до силового центра, 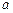 – некоторая постоянная, имеющая размерность длины. Определить среднее расстояние
– некоторая постоянная, имеющая размерность длины. Определить среднее расстояние  частицы от силового центра. [
частицы от силового центра. [  =
=  ].
].
4.27. Записать стационарное уравнение Шредингера для свободной частицы массой 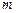 , которая движется вдоль оси
, которая движется вдоль оси 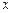 , а также определить посредством его решения собственные значения энергии. Что можно сказать об энергетическом спектре свободной частицы? [
, а также определить посредством его решения собственные значения энергии. Что можно сказать об энергетическом спектре свободной частицы? [  , спектр непрерывный].
, спектр непрерывный].
4.28. Электрон в бесконечно глубоком одномерном прямоугольном потенциальном ящике находится в основном состоянии. Какова вероятность обнаружения электрона в средней трети ящика? [0,609].
4.29. Волновая функция 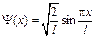 описывает основное состояние частицы в бесконечно глубоком прямоугольном потенциальном ящике шириной
описывает основное состояние частицы в бесконечно глубоком прямоугольном потенциальном ящике шириной  . Вычислить вероятность нахождения частицы в малом интервале ∆
. Вычислить вероятность нахождения частицы в малом интервале ∆  = 0,2
= 0,2  в двух случаях: 1) вблизи стенки
в двух случаях: 1) вблизи стенки  ; 2) в средней части ящика
; 2) в средней части ящика  . [0,052; 0,4].
. [0,052; 0,4].
4.30. Электрон находится в бесконечно глубоком одномерном прямоугольном потенциальном ящике шириной  . Вычислить наименьшую разность энергий двух соседних энергетических уровней (в электронвольтах) электрона в двух случаях: 1)
. Вычислить наименьшую разность энергий двух соседних энергетических уровней (в электронвольтах) электрона в двух случаях: 1)  = 1 мкм; 2)
= 1 мкм; 2)  = 0,1 нм. [1,1∙10-12 эВ; 110 эВ].
= 0,1 нм. [1,1∙10-12 эВ; 110 эВ].
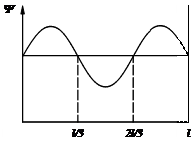
4.31.Вероятность обнаружить частицу на участке (a,b) одномерного потенциально-го ящика с бесконечно высокими стенками вычисляется по формуле  . Если . Если  – функция имеет вид, указанный на рисунке справа, то чему равна – функция имеет вид, указанный на рисунке справа, то чему равна
|
|
вероятность обнаружить частицу на участке 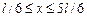 , где , где  – ширина ящика. [2/3]. – ширина ящика. [2/3].
|
4.32. Пучок электронов с энергией Е = 15 эВ встречает на своем пути потенциальный барьер высотой U = 20 В и шириной  =0,1 нм. Определить коэффициент прозрачности потенциального барьера (коэффициент прохождения) D и коэффициент отражения R электронов от барьера (R + D = 1). [D = 0,1; R = 0,9].
=0,1 нм. Определить коэффициент прозрачности потенциального барьера (коэффициент прохождения) D и коэффициент отражения R электронов от барьера (R + D = 1). [D = 0,1; R = 0,9].
4.33. Частица массой 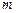 движется в одномерном потенциальном поле
движется в одномерном потенциальном поле  =
=  (гармонический осциллятор). Собственная волновая функция основного состояния гармонического осциллятора имеет вид
(гармонический осциллятор). Собственная волновая функция основного состояния гармонического осциллятора имеет вид 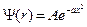 , где
, где  – нормировочный коэффициент;
– нормировочный коэффициент; 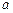 – положительная постоянная. Используя уравнение Шредингера, определить: 1) постоянную
– положительная постоянная. Используя уравнение Шредингера, определить: 1) постоянную 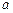 ; 2) энергию частицы в этом состоянии. [
; 2) энергию частицы в этом состоянии. [  ;
;  ].
].

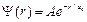 , где
, где  – нормировочный коэффициент волновой функции,
– нормировочный коэффициент волновой функции, 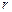 – расстояние электрона от ядра,
– расстояние электрона от ядра, 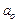 – первый боровский радиус. Определить наиболее вероятное расстояние электрона от ядра в основном состоянии. [
– первый боровский радиус. Определить наиболее вероятное расстояние электрона от ядра в основном состоянии. [  , где
, где 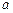 – некоторая постоянная, имеющая размерность длины. Определить среднее расстояние
– некоторая постоянная, имеющая размерность длины. Определить среднее расстояние  частицы от силового центра. [
частицы от силового центра. [  ].
].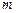 , которая движется вдоль оси
, которая движется вдоль оси 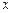 , а также определить посредством его решения собственные значения энергии. Что можно сказать об энергетическом спектре свободной частицы? [
, а также определить посредством его решения собственные значения энергии. Что можно сказать об энергетическом спектре свободной частицы? [  , спектр непрерывный].
, спектр непрерывный].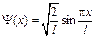 описывает основное состояние частицы в бесконечно глубоком прямоугольном потенциальном ящике шириной
описывает основное состояние частицы в бесконечно глубоком прямоугольном потенциальном ящике шириной  . Вычислить вероятность нахождения частицы в малом интервале ∆
. Вычислить вероятность нахождения частицы в малом интервале ∆  ; 2) в средней части ящика
; 2) в средней части ящика  . [0,052; 0,4].
. [0,052; 0,4]. . Если
. Если  – функция имеет вид, указанный на рисунке справа, то чему равна
– функция имеет вид, указанный на рисунке справа, то чему равна

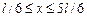 , где
, где  =
=  (гармонический осциллятор). Собственная волновая функция основного состояния гармонического осциллятора имеет вид
(гармонический осциллятор). Собственная волновая функция основного состояния гармонического осциллятора имеет вид 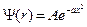 , где
, где  ;
;  ].
].


