Квантовая физика атома
4.37. Уравнение Шредингера для стационарных состояний электрона, находящегося в атоме водорода, задается в декартовых координатах уравнением Представить 1) собственные значения энергии, удовлетворяющие уравнению; 2) график потенциальной энергии взаимодействия электрона с ядром; 3) возможные дискретные значения энергии на этом графике. [1)
4.38. От каких квантовых чисел зависят соответственно радиальная
4.40. Пользуясь условными обозначениями состояний электрона в атоме водорода, записать переходы, приводящие к возникновению серии Бальмера.[ns→2p; nd→2p] (n = 3, 4, …).
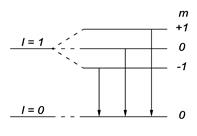
4.41. Объяснить диаграмму, иллюстрирующую расщепление энергетических уровней и спектральных линий (с учетом правил отбора) при переходах между состояниями с 4.42. Нормированная волновая функция, описывающая 4.43. Определить, во сколько раз орбитальный момент импульса электрона, находящегося в d – состоянии, больше, чем для электрона в p – состоянии. [1,73]. 4.44. Записать электронную конфигурацию атома фосфора с вакансией в 2p – подоболочке. [1s2 2s2 2p5 3s2 3p3]. 4.45. Записать квантовые числа, определяющие внешний, или валентный, электрон в основном состоянии атома алюминия. [
|
.
, 
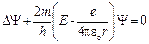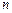=1, 2, 3,… 
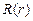и сферическая 
функции, входящие в волновую функцию связанных состояний атома водорода? [ 
; 
].
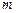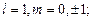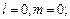
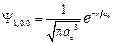s – состояние: 
].
, где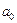 
– первый боровский радиус. Определить среднюю потенциальную энергию электрона в поле ядра. [ 
– 27,2 эВ].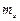
= ±1/2].
