ИНТЕГРАЦИЯ МНЕНИЯ СПЕЦИАЛИСТОВ И СУБЪЕКТОВ ПРОИЗВОДСТВЕННЫХ И РЫНОЧНЫХ ПРОЦЕССОВ 4 страница4. Как изменятся результаты игры, если при прочих равных условиях вероятности состояния природы в рассмотренном примере будут следующими: q 1=0,1; q2=0,15; q3=0,4; q4=0,35 (табл. 30 Пособия). 5. Объясните причины изменения средних выигрышей при разных стратегиях организаторов производства для случаев 1 и 4 (рис. 36 Пособия). 6. Объясните причины изменения средних выигрышей при разных стратегиях организаторов производства для случаев 1 и 5 (рис. 36 Пособия). 7. В чем принципиальная разница максиминного и минимаксного критериев? 8. Какова размерность риска в минимаксном критерии? 9. Как, используя рассмотренные в теме 8 методы, можно определить допустимые затраты производства на сбор дополнительной информации? 10. Какую систему стимулирования персонала, отвечающего за формирование запасов, можно предложить, опираясь на даН' ные матрицы выигрышей (табл. 33 Пособия)? ТЕМА 9. ИСПОЛЬЗОВАНИЕ ИМИТАЦИОННОГО МОДЕЛИРОВАНИЯ И ДЕЛОВЫХ ИГР ПРИ АНАЛИЗЕ ПРОИЗВОДСТВЕННЫХ СИТУАЦИЙ И ПРИНЯТИИ РЕШЕНИЙ § 27. ПРЕДПОСЫЛКИ И УСЛОВИЯ ПРИМЕНЕНИЯ ИМИТАЦИОННОГО МОДЕЛИРОВАНИЯ Принятие решений в сложных производственных и рыночных условиях связано со следующими организационными и методическими трудностями. Во-первых, это традиционный дефицит информации и времени для принятия решения. Во-вторых, в реальном производстве большинство величин являются случайными с разными, а часто и неизвестными законами распределения, и взаимодействует, как правило, не две, а несколько случайных величин. Поэтому чисто аналитические расчеты затруднены или невозможны. В-третьих, опасность и большая стоимость проведения натурных экспериментов на реальной системе с целью оценки вариантов решений, так как система работает в реальном масштабе времени и взаимодействует с многочисленными партнерами и клиентурой потребителями продукции и услуг. В-четвертых, практическая невозможность обеспечения условий сопоставимости при натурном эксперименте, так как он предполагает сравнение двух или нескольких вариантов решений. При сравнении вариантов решений на двух или нескольких предприятиях невозможно обеспечить их равные условия, так как абсолютно сопоставимые аналоги (другие АТП, СТО и т.д.) отсутствуют. Последовательное сравнение нескольких решений на одном производстве также затруднено из-за неминуемого изменения во времени других факторов, влияющих на показатели эффективности, например, спрос на услуги, цены, условиях эксплуатации. В этих условиях при принятии решений можно применять методы исследования и оценки систем на моделях. Модель - это упрощенная форма представления реальных пРоизводственных или рыночных процессов и взаимосвязей в сис- Теме, позволяющая изучить, оценить и прогнозировать влияние 8нешних факторов и составляющих элементов (подсистем) на поучение системы в целом, т.е. изменение целевых показателей. Модели могут быть физическими, математическими, логическими, иМитационными и др. При решении технологических и организационных задач, когда действует много факторов, в том числе и случайных, информация не полная, распространение получил метод имитационного моделирования Имитировать - значит вообразить, постичь суть явления, не прибегая к физическим экспериментам на реальном объекте. Имитационное моделирование - это процесс конструирования модели реальной системы и постановка эксперимента на этой модели с целью: - понимания механизма функционирования системы и взаимодействия подсистем; - выяснения характера реакции системы на изменение внешних факторов; - сравнительной оценки различных стратегий функционирования системы; - оценки показателей эффективности системы (целевых показателей). Имитационное моделирование может производиться: вручную и на ЭВМ. Процесс имитации включает следующие основные этапы: 1) Описание системы, т.е. установление внутренних взаимосвязей, границ, ограничений и показателей эффективности системы, подлежащей изучению. 2) Конструирование модели - переход от реальной системы к определенной логической схеме, отображающей процессы, происходящие в системе. 3) Подготовка и отбор данных, необходимых для построения и работы модели. 4) Трансляция модели, включающая описание модели на языке, используемым ЭВМ. 5) Оценка адекватности, позволяющая судить о корректности выводов, полученных на модели, для реальной системы. 6) Планирование экспериментов: объемов, последовательности. 7) Экспериментирование, заключающееся в реализации на модели имитации реальных процессов и получение необходимых данных. 8) Интерпретация - получение выводов по результатам моделиро* вания. 9) Реализация - практическое использование модели и результатов моделирования при принятии решения для реальной системы. § 28. ПРИМЕНЕНИЕ ИМИТАЦИОННОГО МОДЕЛИРОВАНИЯ ПРИ РЕШЕНИИ ТЕХНОЛОГИЧЕСКИХ И УПРАВЛЕНЧЕСКИХ ЗАДАЧ Рассмотрим принципы имитационного моделирования на примере системы массового обслуживания (СМО), состоящей из одного поста, на который поступают автомобили, требующие ремонта или обслуживания. Прежде всего, напомним из дисциплины «Техническая эксплуатация автомобилей, что СМО - это система, в которой случайными являются моменты поступления требований на обслуживания и продолжительность самих обслуживаний. 1. ХАРАКТЕРИСТИКА ИМИТИРУЕМОЙ СИСТЕМЫ И ПОСТАВЛЕННОЙ ЗАДАЧИ 1) В течение смены Тем на пост поступают автомобили с теми или иными требованиями на ТО или ремонт. Моменты и интервалы между требованиями tMj случайны (рис. 37а) и подчиняются определенному закону распределения f(tM), чаще всего экспоненциальному (рис. 376). 2) Так как техническое состояние автомобилей различно, а требования в общем виде имеют разное содержание и сложность, то продолжительность их выполнения также случайна (рис. 37в) и описывается определенным законом распределения f(tp). Чаще всего нормальным, логарифмически нормальным, Вейбулла или экспоненциальным. 3) В рассматриваемом примере СМО взаимодействуют отказавшие автомобили и пост, на котором выполняются определенные требования по ТО или ремонту этих автомобилей. При этом после поступления на пост 1-го требования возможны три варианта развития событий (рис. 38): I Второе требование поступает в систему обслуживания с интервалом t/2 через некоторое время после завершения выполнения 1-го требования. В этом случае имеет место простой поста в ожидании 2-го требования, равный В общем виде:
II Второе требование возникает в момент завершения работ по обслуживанию 1-го требования. Очевидно, в этом случае СМО работает оинхронно, т.е. нет простоев поста и автомобиля:
В общем виде III Второе требование поступает в систему раньше, чем выполнено первое. При этом автомобиль простаивает в ожидании выполнения первого требованияВ общем виде: 1 4) По такой же схеме СМО работает при поступлении третьего, четвертого и последующих требований их обслуживании. 5) Организаторов производства должна интересовать эффективность работы данной СМО, которая может характеризоваться следующими показателями: - полное время функционирования СМО:
(45) (47) (48) (49) вероятность соответствующих событий и др. В рассмотренной схеме состояние СМО последовательно рассматривается в моменты возникновения (i+1) требования, а критерием для определения состояния системы является соотношение t,(i+1)/tPj(i). 1 Иными словами, начало отчета времени как бы последовательно переносится в очередной момент возникновения требований. Такие имитационные модели называются моделями, использующими переменный временной шаг или шаг до следующего события (появления требований). При этом состояние моделируемой системы обновляется с появлением каждого нового события независимо от интервала времени между этими событиями. По словам Т.Х. Нейлора, моделирование протекает в этом случае во времени событий. 2. ПОСЛЕДОВАТЕЛЬНОСТЬ ПОСТРОЕНИЯ МОДЕЛИ И МОДЕЛИРОВАНИЯ РАБОТЫ СМО 1) Графическое или аналитическое представления схемы взаимодействия случайных величин (рис. 37, 38). 2) Формирование массивов случайных величин, которые обозначаются символом [х]. В примере имеем массивы: - времени выполнения требований [tp]; - интервалов между возникновением требований на обслуживание [tj. Массивы могут формироваться из: - данных фактических наблюдений, т.е. содержать в своем составе
t*, - расчетных значений, полученных из законов распределения случайных величин f(tp) и f(tM); - генерированием, с использованием случайных чисел. Схема получения расчетных значений по законам распределения случайных величин приведена на рис. 39. 3) Имитационное моделирование процесса работы СМО, включающее следующие этапы (рис. 40, 41). [Т] - Установка начального (нулевого) состояния, соответствующего положению, при котором 1-ое требование поступает в самом начале работы СМО, т.е. при t=0 (рис. 40). В принципе можно рассмотреть случай начала обслуживания первого требования при t>0. Это усложнит модель, не увеличивая существенно ее точность. [2j - Извлечение (рис. 41) из массива данных [tp] или генерирование, используя случайные числа и соответствующий закон распределения (рис. 39), продолжительность выполнения очередного требования tp(i).
4) Рассмотренные на рис. 40 циклы имитационного моделирования (начиная с блока 2) повторяются многократно. При этом определяются: число соответствующих реализаций: простоев поста, простоев автомобиля, синхронной работы СМО; определяются принятые показатели эффективности СМО (см. (5) в п. 1). 5) Рассмотренная модель может быть дополнена оценкой экономических последствий вариантов: получению дохода при загрузке поста, убытков при простое поста и автомобиля и др. 6) По результатам моделирования разрабатываются и реализуются меры по совершенствованию работы СМО: увеличение пропускной способности (механизация, увеличение численности исполнителей, продолжительности работы проста и др); регулирование поступления требований в СМО; увеличение числа постов и др.
3. ОЦЕНКА И СФЕРЫ ПРИМЕНЕНИЯ МЕТОДА 1. Преимущества: - оперативность; - малая трудоемкость и стоимость; - сокращение влияния «человеческого фактора»; - возможность многократного повторения опытов; - создание сопоставимых условий при проведении сравнения вариантов решения и др. 2. Недостатки: - сложность построения адекватной модели; - модель лишь примерно отражает реальную производственную ситуацию; - при построении модели используются прошлые данные о системе, а решения и оценки принимаются о будущем системы. 3. Сферы применения метода: - сложные производственные ситуации; - сравнительная оценка альтернативных решений; - оценка действий различных факторов. Примеры применения: - разработка нормативов ТЭА, периодичности, трудоемкости, числа постов; - оценка пропускной способности средств обслуживания и методов её повышения; - определение запасов топлив, материалов, деталей; - оценка вариантов технологических процессов ТО и ремонта; - резервирование площадей, автомобилей, оборудования; - анализ возрастной структуры парков; - определение момента списания или продажи изделия. - оценка эффективности системы массового обслуживания (СМО) и ДР. § 29. ДЕЛОВЫЕ (ХОЗЯЙСТВЕННЫЕ) ИГРЫ Возможность оценивать варианты решений, изменять входные Данные, при необходимости упрощать ситуации позволяет использовать имитационное моделирование при обучении персонала и оценке его квалификации. Например: - При исследовании производительности СМО (постов, участков) участником деловой игры может реализовываться определенная дисциплина очереди: пропускать в первую очередь требования на ремонт автомобилей, дающих наибольший доход, или требования с малой продолжительностью обслуживания. В многоканальных системах возможно перераспределение требований или исполнителей по постам. - С помощью комбинации ряда подобных моделей конструируют имитационные модели зоны, участка, цеха и предприятия и др. - Имитационные модели используются при проведении деловых игр. Деловые (хозяйственные) игры - это метод имитации анализа, принятия и реализации управленческих решений в различных производственных ситуациях. 1) При этом обучающемуся создают ту или иную управленческую или производственную ситуацию, из которой необходимо найти рациональный выход, т.е. принять решение. 2) Критерием является степень приближения решения к оптимальному (которое известно организаторам деловых игр) и время принятия решения. 3) Деловые игры проводятся по определенным правилам, регламентирующим поведение участников, их взаимодействие, критерии эффективности. 4) В роли датчиков, имитирующих реальные производственные ситуации, выступают ЭВМ (человеко-машинная система), наборы карточек случайных событий или ситуации, создаваемые организаторами деловой игры. 5) В деловых играх участвуют специалисты, которые в создаваемых имитационной моделью "производственных ситуациях" принимают решения. Деловые игры используются при обучении и оценке персонала и исследовании сложных производственных систем. При обучении персонала они используются: - для иллюстрации, разъяснения определенных закономерностей, понятий и закрепления знаний; - для программного и целевого обучения определенных специалистов, например, бригадира, диагноста, оператора и др.; - для тренировки специалистов и аварийных бригад в условиях нестандартных «производственных» ситуациях. При обучении персонала деловые игры, как правило, разворачиваются в реальном масштабе времени. При исследовании производственных ситуаций применяется сжатый масштаб времени. Деловые игры позволяют осуществлять предварительный отбор кадров, так как при этом можно оценить способности, профессиональные навыки и знания, пригодность кандидатов на определенные рабочие места и должности специалистов и управленцев. Завершая данную тему необходимо ещё раз подчеркнуть, что даже хорошо сконструированные модели только примерно отражают фунК' ционирование больших систем. Поэтому к полученным с помощью этого метода данным, особенно прогнозам для больших и сложных систем, следует относиться с большой осторожностью. Например, при использовании двух широко применяемых в Европе моделей расхождение в оценке ущерба от среднего легкового автомоби ля парка Бельгии составило 10 - 33% (табл. 36).
ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ ПО ДЕВЯТОЙ ТЕМЕ 1. Постройте блок-схему имитационной модели задачи определения запасов, рассмотренную в теме 8. 2. Сравните эти методы, укажите их преимущества и недостатки. 3. Используя нормированную функцию нормального распределения, постройте массив данных для моделирования случайной величины х, если 11=100, коэффициент вариации V=0,3, число интервалов разбивки случайной величины - 7. 4. Почему необходимо возвращать после реализации случайной величины в массив данных (рис. 41)? 5. Как могут измениться результаты моделирования, если возврат случайных величин в массив данных не произошел? 6. Какой математический аппарат можно использовать для определения необходимого числа реализаций при моделировании? 7. Какие факторы необходимо учитывать при конструировании деловой игры тренировки диспетчера производства, распределяющего отказавшие автомобили между ремонтными участками предприятия? 8. Постройте блок-схему деловой игры для условий предыдущего вопроса. Какие оценочные критерии могут быть применены в этой деловой игре? ТЕМА 10. ЖИЗНЕННЫЙ ЦИКЛ И ОБНОВЛЕНИЕ БОЛЬШИХ ТЕХНИЧЕСКИХ СИСТЕМ § 30. ПОНЯТИЯ О ЖИЗНЕННОМ ЦИКЛЕ СИСТЕМЫ И ЕЕ ЭЛЕМЕНТОВ Развитие экономики связано с постоянным обновлением товаров, изделий и услуг. Любое изделие или услуга зарождаются в ответ на потребности общества, воспроизводятся в течение определенного времени, со временем устаревают, заменяются более совершенными и постепенно изымаются из сферы эксплуатации (применения). Обычно рассматривают жизненные циклы: • Больших систем, например, парк автомобилей определенной модели. • Элементов больших систем, например, конкретного автомобиля. 1. Полный жизненный цикл большой системы, охватывающий науку -> технику -> производство -> эксплуатацию -> списание -> утилизацию, включает следующие основные этапы: 1) Возникновение идеи нововведения на основании осознания потребностей рынка и потребителя, научного предположения, гипотезы или открытия. Например, идея применения газомоторного топлива на транспорте, диктуемая возможным дефицитом жидкого топлива и экологическими требованиями. 2) Выдвижение теории, а применительно к техническим, технологическим и организационным решениям - концепции проекта, затем бизнес-плана, т.е. известной комбинации существующих и новых знаний, методов, технологических и других приемов, которые могут дать необходимый эффект. На этом этапе определяются схемы соответствующих решений, предполагаемый потребитель и масштабы применения нововведения. 3) Проверка теории или концепции проекта путем лабораторного эксперимента, демонстрирующего правильность теории или принципу альную осуществимость проекта. 4) Лабораторная или опытная проверка, обеспечивающая пол£ чение полезного эффекта в принципиально пригодной для практического использования форме. Это может быть модель технического устройства, образец материала, процесс, пробная услуга и т.д. 5) Эксплуатационные испытания или рыночная апробация, демо_Н; стрирующие работоспособность нового технического средства или процесса, возможность достижения заданных целевых нормативов. Для услуг проверяется их восприимчивость и востребованность потенциальным потребителем и уточняется возможный спрос. На основании этого этапа определяются направления доработки или переработки изделия или услуги, уточняются требования к сфере эксплуатации. Например, применительно к газомоторному топливу: создание сети газозаправочных пунктов, переоборудование автомобилей, приспособление производственно-технической базы к обслуживанию газобаллонных автомобилей, подготовка персонала и др. 6) Промышленное (рыночное) внедрение, означающее начало производства нового технического средства или предоставления новой услуги, характеризующее готовность к их практическому применению и гарантирующее получение заданных целевых нормативов эффективности, масштабов применения и др. 7) Широкое внедрение нововведений, позволяющее оценить действительный эффект и рыночную нишу с учетом ряда факторов, которые невозможно было полностью учесть на начальных стадиях, и полностью подготовить эксплуатационную инфраструктуру. 8) Длительное производство и эксплуатация (изделие) или применение (услуга, технология) нововведений, насыщение ими рынка, создание новой системы, например парка автомобилей новой конструкции или интернет-системы приобретения автомобилей, запасных частей и материалов, организации перевозочного процесса. Получение реальной пользы по нововведениям. 9) Постепенная замена (вытеснение) предшественников (изде- лия, услуги, технологии) нововведениями - формирование новой или обновленной большой системы. 10) Устаревание «нововведения», вывод из эксплуатации старых элементов системы и их постепенная замена нововведениями следующего поколения. 11) Утилизация и частичное вторичное использование подсистем и элементов старой системы. Жизненный цикл большой системы - парка автомобилей определённой модели может составить 25-30 лет. 2. Жизненный цикл элементов системы проще и короче жизненного цикла самой системы. Например, жизненный цикл элемента большой системы (автомобильного парка) - автомобиля складывается из его приобретения и обкатки; перевозочного процесса; хранения, технического обслуживания и ремонта; модернизации (при необходимости); списания (перепродажи) и утилизации. Показателем жизненного Цикла элемента является его ресурс, т.е. наработка (часы, км) до списания или реализации. Жизненный цикл элемента системы составляет на примере автомобилей в среднем 7-12 лет, в течение которых технико- эксплуатационные показатели постепенно ухудшаются (табл. 37). Обобщающим показателем качества подержанных автомобилей является их рыночная цена, которая по отношению к новым автомоби • во-первых, обновление большой системы происходит через многократные замены ее элементов; • во-вторых, чем чаще заменяются элементы, тем «моложе» их совокупность в большой системе; • в-третьих, чем «моложе» элементы, т.е. эффективнее, большая система. Следовательно, эффективность большой системы во многом определяется эффективностью ее элементов. А эффективность элементов системы зависит от трёх основных факторов: 1) начального уровня технико-экономических свойств; 2) темпов снижения технико-эксплуатационных свойств элемента при его старении, т.е. увеличении наработки с начала эксплуатации (табл. 37);
3) сроков службы элемента.
Таким образом, мы подошли к понятию возрастной структуры системы, например парка транспортных средств. § 31. ВОЗРАСТНАЯ СТРУКТУРА И РЕАЛИЗУЕМЫЕ ПОКАЗАТЕЛИ КАЧЕСТВА СИСТЕМЫ И ЕЁ ЭЛЕМЕНТОВ Рассмотрим эти понятия на характерном для больших систем примере автомобилей и парков. 1. ВОЗРАСТНАЯ СТРУКТУРА ПАРКА В любом парке эксплуатируются элементы (автомобили), имеющие различную наработку с начала эксплуатации от новых до изделий, подлежащих списанию. Наработка может исчисляться временем t (часы, месяцы, годы), циклами, объёмами выполненной работы, километрами пробега (L) и т.д. Обычно при анализе весь парк разбивается по наработке с начала эксплуатации до списания (ten > Lcn) на «возрастные группы» (табл. 38) и определяется количество элементов например, автомобилей (Aj), принадлежащих к конкретной возрастной группе j (от j=1, до jen) в календарный момент времени i (например, на 1.01. 2001 г.). Привязка к календарному времени необходима, т.к. состав возрастных групп может меняться по времени от соотношения постановки (АП|) списания (Асп*), влияя, таким образом, на размеры групп (Ау). Таблица 38 Возрастная структура крупного московского автобусного парка (i=2000 г.)
|
Рис. 38. Варианты (I, II, III) взаимодействия потока требований и их 9§служивание в СМО
(44)
n iCTcnnc t-ivicHbi, недели, месяца:
m - число случаев простоя поста; полное время работы поста за тот же период времени (Т):
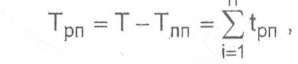П - число обслуживаемых требований; полное время ожидания обслуживания требований в системе:
к - число случаев простоя автомобиля; среднее значение продолжительности разовых реализаций:
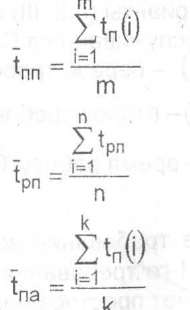
Рис. 40. Блок-схема имитационного моделирования работы поста ТО и ремонта одноканальной СМО
Рис. 41. Схема генерирования реализаций, сравнения случайных величин и идентификации вариантов работы СМО
