ИНТЕГРАЦИЯ МНЕНИЯ СПЕЦИАЛИСТОВ И СУБЪЕКТОВ ПРОИЗВОДСТВЕННЫХ И РЫНОЧНЫХ ПРОЦЕССОВ 5 страница
Таким образом, под возрастной структурой автомобильного парка понимается количественное или процентное распределение его автомобилей по имеющимся возрастным группам (табл. 38) Удельный вес автомобилей данной возрастной группы j в парке в Момент времени i обозначается А „ при где А, - размер парка Aij - количество автомобилей j-й возрастной группы в парке в момент времени i. Необходимо иметь ввиду, что возрастная группировка парка по пробегу лучше отражает надежностные свойства автомобилей, но более сложна в расчетах из-за падения годовой наработки в км при старении автомобилей (рис. 42).
1 - Lr = f(T); 2 - Lp среднегодовой пробег за Т = 16 лет(реализуемый показатель). Специалисту необходимо знать и следить за возрастной структурой парка по следующим причинам: 1) она не постоянна и изменяется во времени в зависимости от соотношений поставок и списания автомобилей; 2) при увеличении наработки автомобиля с начала эксплуатации большинство его технико-эксплуатационных свойств ухудшается: «надежность; • производительность; • экологическая и дорожная безопасность; • топливная экономичность и т.д. Поэтому, оценивая показатели качества автомобилей или парков, следует учитывать возраст автомобиля и парка и использовать предложенное автором понятие реализуемый показатель качества. 2. РЕАЛИЗУЕМЫЙ ПОКАЗАТЕЛЬ КАЧЕСТВА ЭЛЕМЕНТА СИСТЕМЫ Потребителя интересуют не только начальные значения показателей качества, но и то, как они изменяются по мере эксплуатации изделия.
Реализуемый показатель качества элемента системы rikj(t,L) - это средний показатель конкретного его свойства, определённый за заданную наработку (53) где rikj— показатель качества элемента j-той возрастной группы; rij — число возрастных групп, для которых определяется П^. Если доходы автобуса за 100 тыс. км принять за 100%, то за весь срок службы средние доходы составят (табл. 37):
Для первых трех возрастных групп этот показатель равен 94%. 3. РЕАЛИЗУЕМЫЙ ПОКАЗАТЕЛЬ КАЧЕСТВА ПАРКА КАК СИСТЕМЫ Реализуемый показатель качества парка определяется реализуемыми показателями качества элементов различных возрастных групп (rikij), формирующих парк, и возрастной структурой парка в момент i:
где jcn - последняя возрастная группа, подлежащая списанию. Плавило №34 При определенных свойствах автомобиля как подсистемы, т.е. значениях П^ tcn реализуемый показатель качества автомобиля постоянен rikpCOnst, а для парка (системы) он зависит от возрастной структуры ajj, т.е. непостоянен n^^COtlst. На этом основано управление реализуемыми показателями качества парка. Рассмотрим, используя данные табл. 37, пример, иллюстрирующий влияние возрастной структуры парка (табл. 39) на показатели эффективности. Реализуемый показатель - средний простой автобуса за весь срок его службы равен (табл. 39):
к простою автобусов первой возрастной группы (lUUVo). При равномерном распределении парка по возрастным группам (I вариант, табл. 39) реализуемый показатель качества парка в момент i равен:
Т. е. реализуемые показатели качества парка и автобуса равны. Это идеальный вариант, который практически не реализуется, так как среднегодовой пробег автомобилей при старении, как отмечалось выше, не остается постоянным, а сокращается (рис. 42). Равномерное распределение возрастного состава парка по срокам службы возможно при условии, что: а) поставки новых автомобилей соответствуют списанию старых; б) списание осуществляется при одинаковом возрасте автомобилей; в) нет аварийных списаний и передач автомобилей при t<tcnl
г) нет поступления подержанных автомобилей.
т.е. простои в ремонте увеличивается, а показатель качества парка хуже показателя качества автобуса при установленном сроке службы. Третий вариант (i=3, табл. 39) иллюстрирует тенденцию омоложения парка. Для него реализуемый показатель качества автомобиля улучшается
т.е. лучше, чем у автобуса (1bi!u/o). 4. СРЕДНЯЯ НАРАБОТКА ЭЛЕМЕНТОВ ПАРКА С НАЧАЛА ЭКСПЛУАТАЦИИ Кроме распределения парка по возрастным группам возрастную структуру характеризует также средний возраст (Tj) и средний пробег (l|) автомобилей парка с начала эксплуатации на момент i. Средний возраст парка в момент времени i равен:
где Tj - середина интервала j-й возрастной группы автомобилей. В таблице 40 приведен пример расчета среднего возраста парка при изменении его возрастной структуры и времени существования парка. Таблица 40
Аналогично определяется средний пробег автомобилей парка с Начала эксплуатации (L). § 32. УПРАВЛЕНИЕ ВОЗРАСТНОЙ СТРУКТУРОЙ ПАРКА Средний возраст и возрастная структура (ВС) парков отдельных АТП могут существенно изменяться за небольшие промежутки времени, что не может не отразиться на показателях эффективности работы парка в целом и потребных ресурсах: себестоимости, коэффициенте технической готовности и производительности автомобилей, потребности в рабочей силе и базе, запасных частях, т.е. возрастная структура парка влияет на работу ИТС и автомобильного транспорта в целом. Поэтому необходимо, во-первых, прогнозировать характер изменения возрастной структуры парка, во-вторых, уметь управлять возрастной структурой. Правило №35 Под управлением возрастной структурой парка понимается ее прогнозирование и такое целенаправленное изменение, которое обеспечивает получение в необходимый момент времени i заданных реализуемых показателей качества парка ПК|. 1. В общем случае на формирование возрастной структуры парка влияют следующие основные факторы: 1) Исходная возрастная структура, т.е. распределение парка по возрастным группам j в начальный момент i=1: Эц, а-|2, Э^з,... а^; 2) Размер поставки новых автомобилей в момент i = 1,2,3...i: Апь 3) Размер списания автомобилей в те же моменты - Асп.. Отношение размера поставки к размеру парка в i-м году называется коэффициентом пополнения Г, А „ г-. = !_!_ (56) А, Отношение размера списания к размеру парка в i-м году называется коэффициентом списания или выбытия bj:
При Г| =bj имеет мест о пиосше восстановление, а при n > bi расширенное, т.е. парк автомобилей постоянно увеличивается. При П< bj происходит деградация, т.е. сокращение размера парка. Для автомобильного парка США за последние 10 лет коэффициенты Г и Ь составили в % к парку: легковые автомобили - 6,9 и 5,9; грузовые автомобили - 8,4 и 5,6. 4) ресурс (срок службы) автомобиля до списания tcn. На рис. 43 приведена схема изменения размера вновь образованного в момент t=0 парка А, при различном соотношении коэффициентов пополнения и списания и зафиксированном сроке службы автомобиля ten- Это так называемое дискретное списание.
автомобилей при отсутствии списания (кроме аварийного), т.е. Г>0; Ь=0; II - от t=tcn до момента окончания производства (или приобретения данной транспортной фирмой) автомобилей определенной модели (tK). На этом этапе в зависимости от соотношения г и b может наблюдаться относительный рост парка Г > Ь (1, рис. 43), его стабилизации г = b (2, рис. 43) или при г < b - сокращении размера (3, рис. 43); III - от tK до tK + tcn (рис. 43) постепенная ликвидация парка данных автомобилей (Г = 0; Ь > 0). Схема изменения реализуемых показателей качества (например, коэффициента технической готовности, затрат на обеспечение работоспособности) при Г=Ь на втором этапе приведена на рис. 43,6. 2. Следует различать регулирование и управление возрастом и возрастной структурой парков. Регулирование ВС проводится на общегосударственном уровне и сводится к установлению такой амортизационной, налоговой, таможенной и лизинговой политики, которая способствует или препятствует быстрому обновлению парков. Управление ВС проводится на уровне конкретных предприятий и фирм и сводится к регулированию процессов списания- пополнения и соотношений в парке изделий разных возрастных групп при условии обеспечения требуемого (заданного) для парка объема транспортной работы при минимальных затратах или максимальной прибыли. При изменении сроков службы меняются эксплуатационные затраты и капиталовложения. Так, при сокращении установленных сроков службы уменьшаются затраты на ТО и ремонт, потребность в персонале и ПТБ для ТО и ремонта, потребность и затраты на запасные части, сокращается их номенклатура. Но одновременно увеличивается поставка новых автомобилей, т.е. растут амортизационные отчисления для АТП и капиталовложения в промышленность для расширения производства автомобилей (табл. 41). Из приведенных в табл. 41 данных следует, что сокращение сроков службы грузовых автомобилей средней грузоподъёмности с 10... 12 до 5...7 лет позволяет при том же объеме выполненной транспортной работы: • на 20...25% сократить инвентарный состав парка; • на 8... 15% уменьшить потребность в капитальном ремонте основных агрегатов; • на 25...30% сократить потребность в рабочей силе на ТО и TP автомобилей в эксплуатации; • на 23...40% уменьшить расход запасных частей; • на 14...20% уменьшить приведенные затраты. При этом годовые поставки новых автомобилей должны быть увеличены в 1,5... 1,9 раза, что требует существенных инвестиций.
Необходимость "омоложения" автомобильных парков диктуется безопасностью движения, экологическими и экономическими требовз- ниями. Кроме того, сокращение сроков службы позволяет интенсифицировать процесс внедрения новых конструкций автомобилей, т. е. способствует НТП и повышению технического уровня парка.
§33. МЕТОДЫ РАСЧЕТА ПОКАЗАТЕЛЕЙ ВОЗРАСТНОЙ СТРУКТУРЫ АВТОМОБИЛЬНЫХ ПАРКОВ 1. МЕТОДЫ РАСЧЁТА ПОКАЗАТЕЛЕЙ ВС Методы расчета возрастной структуры парка зависят от принятого способа списания и поставки изделий: Дискретное списание - по достижении установленной или принятой в данном предприятии наработки (срока службы ten или пробега) происходит списание или продажа в другие руки автомобиля вне зависимости от его технического состояния или показателей работы. Такая схема распространена при интенсивной эксплуатации в условиях повышенных требований к надежности (междугородные и международные перевозки, пассажирские перевозки, экстренная доставка ценных грузов и т.д.); Случайное списание (рис. 44), характеризуется вариацией фактической наработки до списания f(t). По этой схеме списание производится на основании контроля за определенными показателями работы автомобиля, например, по изменению производительности, уменьшению прибыли, накопленному расходу запасных частей и т.д.
1) Различают календарное время существования парка автомобилей данной модели i и возрастную группу автомобилей j. Год начала образования парка или исходный год анализа его возрастной структуры принимается равным i=1. 2) Возраст автомобиля (j) и календарное время существования данного парка (i) измеряются в одинаковых условных или абсолютных единицах, например годах. 3) При изменении календарного времени на одну единицу (i+1) автомобили, имевшие в момент i возраст j, "стареют" на одну единицу и переходят в следующую возрастную группу (j+1), т.е. происходит диагональный сдвиг. Например, если в 2000 г. (i=1) автомобиль имел возраст j=4 года (выпущен в 1997 г.), то в 2001 г. (i=1+1=2) его возраст составит 4+1 =5 лет. 4) Поставки автомобилей условно относятся к началу соответствующе го периода года, а списание к концу года.
5) Если приобретаются только новые автомобили АПи, а списываются автомобили при t=tcn. т.е. Ас, = АцСп, то дискретное списание называется простым. Количество автомобилей (j+1) возрастной группы в момент (i+1) определяется по правилам диагонального сдвига (рис. 45) и с учетом этапов существования парка (рис. 43). Для I этапа (при i=t<tcn) в первой возрастной группе 0=1) в момент (i+1) поступит автомобилей: В последующих возрастных группа:Ау (59) Списания на этом этапе нет, т.е., Для II этапа (при tcn< i < tK) расчеты проводятся по тем же формулам (58) и (59), но дополнительно появляется группа автомобилей, подлежащих списанию: ACj+i = Ац (60) Для III этапа (tK+tcn) > t > tK поставки новых автомобилей прекращаются АП(|+1)1= 0, размеры промежуточных возрастных групп ато- мобилей определяются по формуле (59), а размер списания по формуле (60). В табл. 42 рассмотрен пример трансформации структуры и размеров парка при простом и сложном обновлении для двух временных разрезов i и i+1 и сроков службы изделий tcn=5 лет. Исходная возрастная структура парка (при i=1) зафиксирована во втором столбце таблицы. Структура парка при временном разрезе i+1, простом обновлении и поставке 8 новых автомобилей приведена в третьем столбце, а структура при сложном обновлении, заключающаяся в приобретении 20 автомобилей третьей возрастной группы - АП(,+1)з, в четвертом столбце. Если при tcn = 5 лет в 2001 г. (i=1) первая возрастная группа в парке насчитывала Ац=6 автомобилей, вторая А12=12, А13=22, А14=28, А-|5=16, а в течение 2002 г. предполагается приобрести 8 новых автомобилей Ап(|+1)1=Ап21=8, то распределение автомобилей по группам в 2002 г. (i=2) будет следующим: 6) Если допускается приобретение автомобилей не только новых, но и промежуточная продажа и покупка (или лизинг), то дискретное списание и восстановление является сложным. При этом количество, автомобилей (j+1) возрастной группы в момент времени (i+1) определяется следующим образом
где An(i+i)(j+i) - поставка в момент (i+1) автомобилей возрастной группы 2 < j < tcn, т.е. неновых, которые суммируются к соответствующей возрастной группе; AC(j+1)(j+i) - вывод из эксплуатации (продажа, передача в лизинг и т.д) в момент времени (i+1) автомобилей возрастной группы 2<j<t сп, которая вычитается из соответствующей возрастной группы. Размеры первой возрастной группы при наличии поставок новых автомобилей и размеры списания определяются по формулам (58) и (59). Естественно, что в реальных условиях в конкретные моменты i существования парка некоторые члены формул, например, размер поставок или списания, могут быть равны нулю. 7) Как при простом, так и при сложном списании в каждом временном разрезе количество приобретенных и списанных автомобилей в общем случае (характерном для реальной практики) не равно, т.е, An,*ACi. 8) Размер парка определяется суммированием всех данных по столбцам: 9) Прогнозирование возрастной структуры парка позволяет определить по формулам (54) и (62) размер и динамику изменения реализуемого показателя качества парка по показателям качества автомобилей различных возрастных групп. Так, если доходы автобусов разных возрастных групп парка определяются в процентах согласно табл. 37. Di=100; D2=99; D3=82; D4=64; Ds=41, то реализуемый показатель качества парка автобусов в момент i (табл. 42) по доходам с учетом возрастной
относительно доходности (100%) новых автобусов (j=1). При временном разрезе i+1 и простом восстановлении доходность среднего автомобиля парка равна D,+i =64,9%, т.е. на 9,7% ниже, чем при исходной структуре (i). При представленном в табл.42 варианте сложного обновления (приобретении не новых, а автобусов 3-й возрастной группы) реализуемый показатель качества по доходности парка будет еще ниже и составит 65% от доходности D, =100% автобусов первой возрастной группы, хотя общий доход в результате роста парка возрастет. 10) Средний возраст парка Т определяется по формуле (47) Для разреза i имеем
Для того же разреза и сложном обновлении парка поставкой 20 автомобилей третьей возрастной группы средний возраст парка будет еще выше и составит: T(i+i> = 3,32 года. Это существенно увеличивает затраты на его содержание. 11) Относительная масса дохода парка (в условных единицах) составляет: MD| = D(-A,. (63) По вариантам это составит: - исходный (i) - простое обновление (i+1) - сложное обновление (i+1)
Фрагмент расчета простого и сложного дискретного обновления парка
Таким образом в рассмотренных примерах (см. табл. 42): простого обновления масса дохода сократится на 18% в результате старения и сокращения размера парка на 9%. сложного обновления масса дохода по сравнению с исходной сократилась примерно на 4% при росте размера парка на 10% и его старении на 11%, что приведет к существенному увеличению расходов на содержание этого парка. Правило № 36. Оценивая изменения возрастной структуры парка, можно прогнозировать изменение во времени всех реализуемых показателей парка, а именно размера, возраста, уровня надежности, дохода, расходов и т.д. Это создает надежную информационную базу для принятия решения по необходимым размерам закупки и списания подвижного состава, планированию расходов, необходимости модернизации производственной базы, дополнительной потребности или излишке рабочей силы и оборудования. 2. РАСЧЕТ ПОКАЗАТЕЛЕЙ ВС ПАРКА ПРИ СЛУЧАЙНОМ СПИСАНИИ И КОМПЕНСАЦИОННОМ ПОПОЛНЕНИИ Этот расчет основан на использовании закономерностей процесса восстановления (закономерности 5-го вида, изученные в разделе теоретических основ дисциплины "Техническая эксплуатация автомобилей"). При этом весь наличный парк рассматривается в качестве восстанавливаемой технической системы, состоящей из элементов - отдельных автомобилей. Случайное списание автомобиля в соответствии с законом распределения (рис. 44) - это как бы отказ системы, а поставка нового автомобиля, заменившего списанный, - восстановление системы. Поток замен списываемых автомобилей во время существования парка i описывается, как это было показано в теоретических основах ТЭА, ведущей функцией fi(i) и параметром потока отказов (списаний) и замен (поставок) Ш(|). Ведущая функция определяет накопленное число событий (в данном случае замен списанных автомобилей) к определенной наработке i большой системы - парка автомобилей. Разница Пр+и - Q(i) =гП{Хо определяет число событий в интервале наработок восстанавливаемого элемента системы (i+1) - i. Для этого случая где Fk - интегральная функция распределения наработки при k-й замене инвентарного автомобиля парка; i - календарное время работы парка. Смысл этого выражения состоит в том, что за фактический календарный срок существования парка автомобилей данной конструкции (i=20.. 25 лет) будет несколько (к) списаний и замен каждого списочного В случае нормального закона распределения наработки до списания автомобиля функция fi(i) может быть определена аналитически по следующей формуле- (65) где X - средняя наработка до списания автомобиля; ст - среднеквадратические отклонения наработки до списания; к - число замен каждого списочного автомобиля; Ф(г) - нормированная функция, определяемая по стандартной таблице (см. прилож. 6) для выражения: Рассмотрим пример последовательности
Интервал календарного времени существования парка принят в 1 год, т.е. размер списания и компенсирующей поставки определяется в расчете на 1 год. Расчет проводится для i=16, т.е. 16 календарных лет существования парка. Заданный среднегодовой размер парка, который необходимо поддерживать по требованиям коммерческой эксплуатации, Aj = const = 100 автомобилей. Последовательность расчета: 1) Определяем число замен в первом календарном интервале работы парка: а) для первых замен (i=1,k=1, Х=5, ст=1,5) имеем:
|

 в момент времени i, являющийся календарным временем существования данного парка;
в момент времени i, являющийся календарным временем существования данного парка; Наработка с начала эксплуатации, годы
Рис. 42. Изменение среднего годового пробега (l_r) легкового автомобиля в Швеции в зависимости от наработки с начала эксплуатации
Наработка с начала эксплуатации, годы
Рис. 42. Изменение среднего годового пробега (l_r) легкового автомобиля в Швеции в зависимости от наработки с начала эксплуатации


 (54)
(54) по отношению
по отношению

 Реализуемый показатель качества парка:
Реализуемый показатель качества парка:

 (55)
(55) года
года (57)
(57) Рис. 43. Схема изменения размера (а) и реализуемого показателя качества (б) парка: А, - размер парка;
Пи - реализуемые показатели качества;
4 - коэффициент технической готовности ат;
5 - затраты на обеспечение работоспособности.
При этом наблюдаются три характерных этапа:
Рис. 43. Схема изменения размера (а) и реализуемого показателя качества (б) парка: А, - размер парка;
Пи - реализуемые показатели качества;
4 - коэффициент технической готовности ат;
5 - затраты на обеспечение работоспособности.
При этом наблюдаются три характерных этапа:
 рост парка, вызванный поставкой новых
рост парка, вызванный поставкой новых
 Рис. 44. Распределение наработки до списания легковых (1) и грузовых автомобилей большой грузоподъемности (2) автомобильного парка США
Рис. 44. Распределение наработки до списания легковых (1) и грузовых автомобилей большой грузоподъемности (2) автомобильного парка США

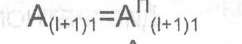 (58)
(58)
 а списано будет 16 автомобилей.
а списано будет 16 автомобилей. (61)
(61) (62)
(62)

 Таблица 42
Таблица 42
 (64)
(64)
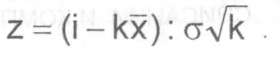 расчета случайного списания при следующих исходных данных:
расчета случайного списания при следующих исходных данных:



