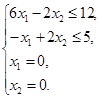Строят многоугольник решений.
4. Строят вектор 5. Строят начальную прямую Определяют координаты точки максимума функции и вычисляют значение целевой функции в этой точке. Минимальное значение линейной функции цели находится путем передвижения начальной прямой противоположном вектору Пример Найти максимум и минимум линейной функции:
Решение; Построим на плоскости Для этого в неравенствах системы ограничений и условиях неотрицательности переменных знаки неравенств заменим на знаки точных равенств.
Построив полученные прямые, найдем соответствующие полуплоскости и их пересечение
Построив полученные прямые, найдем соответствующие полуплоскости и их пересечение
|
, направление которого указывает на возрастание целевой функции.
и передвигают ее в направлении вектора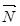 
до крайней угловой точки многоугольника решений. В результате находят точку, в которой целевая функция принимает максимальное значение, либо множество точек с одинаковым максимальным значением целевой функции, если начальная прямая сливается с одной из сторон многоугольника решений, либо устанавливают неограниченность сверху функции на множестве планов 
.
при условиях:
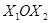многоугольник решений рис.1.
