Многоугольником решений задачи является пятиугольник АВ-СДЕ, координаты точек которого удовлетворяют условию неотрицательности и неравенствам системы ограничений задачи.Для нахождения точек экстремума построим начальную прямую
Решив систему уравнений, получим:
Для нахождения минимального значения целевой функции задачи перемещаем начальную прямую в направлении, противоположном вектору значение в угловой точке Е, где Найдем координаты угловых точек В, Д и А. Для этого решим следующие системы уравнений:
В результате получим координаты точек В (0;2,5), Д (2,0) и А (0,1). Вычислим значения целевой функции во всех угловых точках многоугольника решений АВСДЕ:
КОНТРОЛЬНЫЕ ВОПРОСЫ Сформулируйте общую задачу линейного программирования. 2. Дайте определение невырожденного и вырожденного опорного плана, оптимального плана. 3. Какое множество называется выпуклым? 4. Какая точка выпуклого множества называется угловой?
|
и вектор 
. Передвигая прямую 
параллельно самой себе в направлении вектора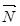 
, найдем точку С, в которой начальная прямая принимает положение опорной прямой. Следовательно, в точке С целевая функция принимает максимальное значение, так как точка С получена в результате пересечения прямых 1 и 2, то ее координаты удовлетворяют уравнениям этих прямых:
