Элемент симплексной таблицы, находящейся на пересечении ведущих столбца и строки, называют разрешающими и выделяет кружком.
5. Построение нового опорного плана Переход к новому плану проводится пересчетом симплексной таблицы по методу Жордана-Гаусса. Сначала заменим переменные в базисе, т.е. вместо Разделим все элементы ведущей строки предыдущей симплексной таблицы на разрешающий элемент и результаты деления занесем в строку следующей симплексной таблицы, соответствующую введенной в базис переменной нового плана находятся по правилу прямоугольника: где А и В - элементы старого плана, образующие прямоугольник с элементами
6. Полученный новый опорный план опять проверяется на оптимальность в соответствии с этапом 3 алгоритма. При решении задачи линейного программирования на минимум целевой функции, признаком оптимальности плана является отрицательные значения всех коэффициентов индексной строки симплексной таблицы. Если в направляющем столбце все коэффициенты Если в столбце симплексной таблицы содержатся два или несколько одинаковых наименьших значения, то новый опорный план будет вырожденным (одна или несколько базисных переменных станут равными нулю). Вырожденные планы могут привести к зацикливанию, т.е. многократному повторению процесса вычислений, не позволяющему завершить задачу. С целью исключения этого для выбора направляющей строки используют способ Креко, который заключается в следующем. Делим элементы строк, имеющие одинаковые наименьшее значение Если в оптимальный план вошла дополнительная переменная Если в индексной строке симплексной таблицы оптимального плана находится нуль, принадлежащий свободной переменной, не вошедшей в базис, а в столбце, содержащем этот нуль, имеется хотя бы один положительный элемент, то задача имеет множество оптимальных планов. Свободную переменную, соответствующую указанному столбцу, можно внести в базис, выполнив соответствующие этапы алгоритма. В результате будет получен второй оптимальный план с другим набором базисных переменных.
ПРИМЕР РЕШЕНИЯ ЗАДАЧИ СИМПЛЕКСНЫМ ДЕТОДОМ. Торговое предприятие, располагающее материально-денежными ресурсами, реализует три группы товаров А, В и С. Плановые нормативы затрат ресурсов на тыс. руб. товарооборота, прибыль от продажи товаров на тыс. руб. товарооборота, а также объем ресурсов заданы в таблице 2. Определить плановый объем продажи и структуру товарооборота так, чтобы прибыль торгового предприятия была максимальной. Таблица 2
1.Запишем математическую модель задачи. Определить
|

 в базис войдет переменная
в базис войдет переменная  , соответствующая направляющему столбцу.
, соответствующая направляющему столбцу. -
-  ,
, элемент старого плана,
элемент старого плана,  разрешающий элемент,
разрешающий элемент, и
и  .
.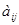
 0,то функция цели
0,то функция цели  неограниченна на множестве допустимых планов, т.е.
неограниченна на множестве допустимых планов, т.е. 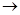
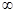 и задачу решить нельзя.
и задачу решить нельзя. , на предполагаемые разрешающие элементы, а результаты заносим в дополнительные строки. За ведущую строку выбирается та, в которой раньше встречается меньшее число при чтении таблицы слева направо по столбцам.
, на предполагаемые разрешающие элементы, а результаты заносим в дополнительные строки. За ведущую строку выбирается та, в которой раньше встречается меньшее число при чтении таблицы слева направо по столбцам. , то при реализации такого плана имеются недоиспользованные ресурсы
, то при реализации такого плана имеются недоиспользованные ресурсы  гo вида в количестве, полученном в столбце свободных членов симплексной таблицы.
гo вида в количестве, полученном в столбце свободных членов симплексной таблицы.
 , который удовлетворяет условиям
, который удовлетворяет условиям



