И обеспечивают максимальное значение целевой функции
Для построения первого опорного плана систему неравенств, приведем к системе уравнений.
В матрице этой системы уравнений
Векторы
Соответствующие этим векторам переменные Решим систему уравнений относительно базисных переменных.
Функцию цели запишем в виде:
2.Полагая, что свободные переменные
Следовательно товары не продаются и прибыль равна нулю, а ресурсы не используются. Заносим первый опорный план 1 в симплексную таблицу 3.
Симплексная таблица 3 Первый опорный план 1 не оптимальный, так как в индексной строке находятся отрицательные коэффициенты - -3,-5,-4. За ведущий столбец выберем столбец, соответствующий переменной |- 5| >
Следовательно, первая строка является ведущей.
|
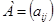имеет:
- линейно независимы, так как определитель, составленный из компонент этих векторов, отличен от нуля:
будут базисными.
=0, 
=0,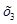 
=0, получим первый опорный план
=(0,0,01100,120,8000), F 
= 0, в котором базисные переменные 
=1100, 
=120,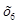 
=8000,
Инд. строка
|- 3I, |- 4I} Рассчитываем значения 9 по строкам, как частное от деления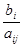 
и выбираем наименьшее:
