Разрешающий элемент равен 0,2 и находится на пересечении ведущего столбца и ведущей строки и выделен кругом.
5. Формируем следующую симплексную таблицу. Вместо переменной Таким образом в новом плане II заполнены строки
Элементы строки определяются аналогично:
Все элементы, расположенные на пересечении строк и столбцов, соответствующих одновременным базисным элементам равны 1, остальные элементы столбца в базисах векторов, включая индексную строку, равны 0. Аналогично проводятся расчеты по всем строкам таблицы, включая индексную. Выполняя последовательно веб этапы алгоритма, формируем план II. 6.На третьей интеракции таблицы 3 получаем план III, который является оптимальным, так как все коэффициенты в индексной строке Оптимальный план можно записать так: X = (250,5375,0,0,0,1875), Следовательно, необходимо продавать товаров первой группы А 250 ед., а второй группы В - 5375 ед. При этом торговое предприятие получает максимальную прибыль в размере 27625 тыс. руб. Товары группы С не реализуются. "В оптимальном плане среди базисных переменных находится дополнительная переменная В индексной строке оптимального плана в столбцах переменных
КОНТРОЛЬНЫЕ ВОПРОСЫ 1. Какие задачи линейного программирования можно решать симплексным методом? 2. Каков признак оптимальности в симплексном методе? 3. Как строится первый опорный план? 4. Как определяется ведущий столбец и ведущая строка симплексной таблицы? 5. Как осуществляется пересчет элементов симплексной таблицы? 6. Каковы особые случаи при реализации симплексного метода?
|

 в план II войдет переменная
в план II войдет переменная  . Строка, соответствующая переменной
. Строка, соответствующая переменной  . На месте разрешающего элемента в плане II получаем 1. В остальных клетках столбца
. На месте разрешающего элемента в плане II получаем 1. В остальных клетках столбца  , которое указывает на место расположение нового
, которое указывает на место расположение нового  в новом плане II. Третий элемент А =1100 и четвертый элемент В =-5 завершают построение прямоугольника в недостающих двух вершинах и расположены по другой диагонали. Значение нового элемента в плане II находится из выражения:
в новом плане II. Третий элемент А =1100 и четвертый элемент В =-5 завершают построение прямоугольника в недостающих двух вершинах и расположены по другой диагонали. Значение нового элемента в плане II находится из выражения:


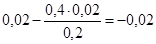

 0.
0. 27625 тыс. руб.
27625 тыс. руб.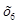 .Это указывает, что ресурсы третьего вида (площадь складских помещений) недоиспользована на 1875 м2, так как переменная
.Это указывает, что ресурсы третьего вида (площадь складских помещений) недоиспользована на 1875 м2, так как переменная  не вошедших в состав базисных, получены ненулевые элементы, поэтому оптимальный план задачи линейного программирования является единственным.
не вошедших в состав базисных, получены ненулевые элементы, поэтому оптимальный план задачи линейного программирования является единственным.


