Игровые методы и модели в экономике
При изучении этой темы следует иметь ввиду, что при решении задач возникает необходимость выбора оптимального экономического решения не только в условиях определенности, но и в условиях риска и неопределенности. Особенностью таких условий является неясность исходов, последствий выбираемых решенииодной стороной, обусловленных или влиянием случайных факторов, или неизвестностью поведения, реакции, например, покупателей на новые виды товаров; неясностью погодных условий при перевозки грузов; недостаточной информированностью о торговых операциях, закупках, сделках; наличием очень большого числа вариантов поведения противоположной стороны. В таких случаях наблюдаются разнообразные по своей природе противоречия или столкновения интересов, целей ит.д. участвующих сторон. Решением подобного рода задач и занимается теория игр и статистических решений, позволяющая находить оптимальные решения в условиях риска и неопределенности. Схематизированное описание (математическая модель) конфликтной ситуации называется игрой; стороны - участники конфликта (отдельные лица или коллективы) называются игроками, а исход конфликта выигрышем. Задача состоит в выборе такого решения, которое обеспечивает наибольший выигрыш или наименьший проигрыш. Неопределенность в коммерческой деятельности связана с действием заранее непредсказуемых внешних и внутренних факторов в процессе работы организаций и предприятий. В этом случае между сторонами, участниками отсутствует "антагонизм", и такие ситуации называют "играми с природой", а решаются с помощью методов теории статистических решений. Первая сторона (например, торговая организация) выбирает решение стратегии, а вторая сторона "природа" не оказывает первой стороне сознательного, активною противодействия, но ее реальное поведение неизвестно. Пусть Все показатели игры записываются в виде матрицы Неоднозначность и неопределенность условий (в силу вероятного описания) не позволяют получить одну количественную (единую) оценку вариантов решений. Более наглядный показ условий неопределенности дают характерные оценки платежной матрицы, получаемые для конкурирующих вариантов. Каждая из этих оценок является односторонней и не внушает полного доверия, однако вычисление их для анализа необходимо. Рассмотрим наиболее интересные из них. Минимальный выигрыш:
определяется как наименьшая из величин в строке (наиболее пессимистическая оценка). Максимальный выигрыш:
Определяется как наибольшая из величин строки платежной матрицы и характеризует то наилучшее, что дает выбор этого варианта При анализе "игры с природой" вводится показатель, позволяющий оценить, насколько то или иное состояние "природы" влияет на исход ситуации. Этот показатель называется риском Риском Пользуясь этими положениями, строим матрицу рисков Теперь можно записать еще одну характерную оценку: максимальное значение риска для каждого решения
Для решения игровых задач существуют специальные Критерии принятия решения. 1. Критерий, основанный на известных вероятностях состояния: природы, например, покупательского спроса, по данным анализа за прошлые годы: а) если в этом случае известны вероятности состояний «природы»
и при этом полагаем, что
а оптимальной стратегией считается такая, для которой этот показатель эффективности имеет максимальное значение, т.е.
б) если каждому решению
а оптимальной является такая стратегия, для которой получается максимальная величина
В этом случае можно пользоваться значением среднего риска
который следует выбрать минимальным, т.е. определить такую стратегию Т, для которой величина г обращается в минимум:
2.Максиминный критерий Вальда. Выбирается решение торговой организации
|

 коммерческое предприятие имеет m стратегий:
коммерческое предприятие имеет m стратегий:  и допустим имеется n возможных состояний "природы":
и допустим имеется n возможных состояний "природы":  . Поскольку "природа" не является заинтересованной стороной, исход любого сочетания поведения сторон можно оценить с помощью выигрышей
. Поскольку "природа" не является заинтересованной стороной, исход любого сочетания поведения сторон можно оценить с помощью выигрышей  , первой стороны для каждой парк стратегий
, первой стороны для каждой парк стратегий 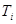 ,- и
,- и  .
.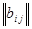 , котораяназывается платежной.
, котораяназывается платежной.

 .
. .
.
 ,
, , то в качестве показателя эффективности стратегии
, то в качестве показателя эффективности стратегии  ,
,
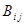 с вероятностями соответственно
с вероятностями соответственно  , то среднее значение выигрыша определяется по формуле:
, то среднее значение выигрыша определяется по формуле: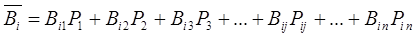 ,
,
 ,
,
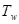 , при котором гарантируется максимальный выигрыш в наихудших условиях:
, при котором гарантируется максимальный выигрыш в наихудших условиях: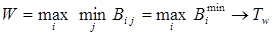 .
.


